На рисунках схематически представлены графики распределения плотности вероятности по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний электрона с различными значениями главного квантового числа n:
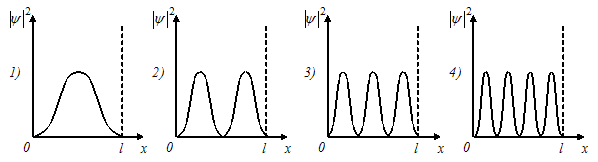
В состоянии с n = 2 вероятность обнаружить электрон в интервале от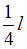
до 
равна …
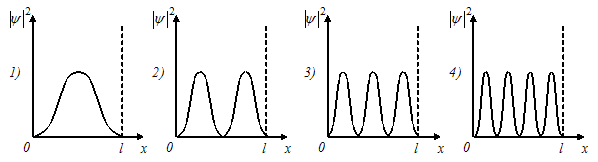
В состоянии с n = 2 вероятность обнаружить электрон в интервале от
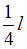до равна …
- ✓
Вероятность обнаружить микрочастицу в интервале (a, b) для состояния, характеризуемого определенной 
-функцией, равна 
. Из графика зависимости 
от х эта вероятность находится как отношение площади под кривой 
в интервале (a, b) к площади под кривой во всем интервале существования 
, то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости 
: n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с n = 2 вероятность обнаружить электрон в интервале от 
до 
равна 
.
-функцией, равна . Из графика зависимости от х эта вероятность находится как отношение площади под кривой в интервале (a, b) к площади под кривой во всем интервале существования , то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости : n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с n = 2 вероятность обнаружить электрон в интервале от до равна .