Даны математические предложения:
«Средней линией треугольника называется отрезок, соединяющий середины двух его сторон»;
«Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны»;
«Два треугольника подобны, если два угла одного треугольника равны двум углам другого треугольника»;
«Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной».
Среди этих предложений есть …
«Средней линией треугольника называется отрезок, соединяющий середины двух его сторон»; «Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны»; «Два треугольника подобны, если два угла одного треугольника равны двум углам другого треугольника»; «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной».Среди этих предложений есть …
- ✓ 1 определение, 2 теоремы, 1 аксиома
Аксиома – это предложение, принимаемое без доказательства. В аксиомах раскрываются свойства основных понятий, таких как «точка», «прямая», «плоскость» и т.д.
Теорема – это утверждение, истинность которого устанавливается с помощью доказательства.
Определение раскрывает смысл некоторого понятия. Например, «отрезок – это часть прямой, ограниченная двумя точками».
Среди данных предложений одно является аксиомой, а именно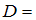
«Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» (аксиома параллельности). Одно предложение является определением (так как в тексте есть слово «называется»): 
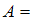«Средней линией треугольника называется отрезок, соединяющий середины двух его сторон».
Два других предложения являются теоремами планиметрии: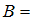
«Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны» и 
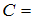«Два треугольника подобны, если два угла одного треугольника равны двум углам другого треугольника».
Таким образом, среди данных математических предложений есть 1 определение, 2 теоремы, 1 аксиома.
Теорема – это утверждение, истинность которого устанавливается с помощью доказательства.
Определение раскрывает смысл некоторого понятия. Например, «отрезок – это часть прямой, ограниченная двумя точками».
Среди данных предложений одно является аксиомой, а именно
«Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» (аксиома параллельности). Одно предложение является определением (так как в тексте есть слово «называется»): «Средней линией треугольника называется отрезок, соединяющий середины двух его сторон». Два других предложения являются теоремами планиметрии:
«Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны» и «Два треугольника подобны, если два угла одного треугольника равны двум углам другого треугольника».Таким образом, среди данных математических предложений есть 1 определение, 2 теоремы, 1 аксиома.
