График функции плотности распределения непрерывной случайной величины, которая задана условием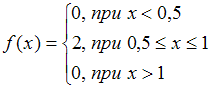 
, имеет вид …
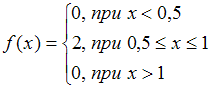, имеет вид …
- ✓
Согласно условию, плотность распределения непрерывной случайной величины имеет вид:
.
Таким образом, при
и при 
значение функции равно 0, то есть графически мы получим объединение двух интервалов вида 
и 
, принадлежащих оси абсцисс. Так как при 
значение функции равно 2, то графически мы имеем отрезок, состоящий из точек вида 
, где 
, 
. Всем этим условиям удовлетворяет только следующий график:
.
.Таким образом, при
и при значение функции равно 0, то есть графически мы получим объединение двух интервалов вида и , принадлежащих оси абсцисс. Так как при значение функции равно 2, то графически мы имеем отрезок, состоящий из точек вида , где , . Всем этим условиям удовлетворяет только следующий график:.