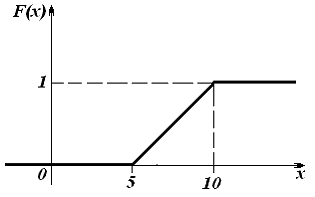
График функции распределения непрерывной случайной величины имеет вид:
.
Тогда значение, которое не может принимать случайная величина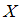
, равно …
.Тогда значение, которое не может принимать случайная величина
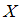, равно …
- ✓ 1
Согласно определению, непрерывная случайная величина 
задается функцией распределения 
, выражающей вероятность того, что 
принимает значение, меньшее, чем 
:
.
Вероятность принятия случайной величиной значения, которое меньше наименьшего из возможных значений, равна 0, поскольку это невозможно. Таким образом, мы должны рассмотреть все точки графика функции, для которых ордината (то есть значение функции) равна 0.
Эти точки образуют луч
на оси абсцисс. При дальнейшем увеличении значения 
значение функции становится отличным от 0. Это значит, что принятие случайной величиной значений, меньших, чем 
, невозможно. Поэтому наименьшее из возможных значений, которые может принимать рассматриваемая случайная величина, равно 5. Очевидно, что из всех указанных значений этому условию удовлетворяет только 1.
Заметим, что вероятность того, что случайная величина
примет значения, не большие 10, равна 1. Таким образом, случайная величина 
может принимать значения только в диапазоне от 5 до 10. Поэтому она может принимать значения 6, 7 и 9.
задается функцией распределения , выражающей вероятность того, что принимает значение, меньшее, чем :.Вероятность принятия случайной величиной значения, которое меньше наименьшего из возможных значений, равна 0, поскольку это невозможно. Таким образом, мы должны рассмотреть все точки графика функции, для которых ордината (то есть значение функции) равна 0.
Эти точки образуют луч
на оси абсцисс. При дальнейшем увеличении значения значение функции становится отличным от 0. Это значит, что принятие случайной величиной значений, меньших, чем , невозможно. Поэтому наименьшее из возможных значений, которые может принимать рассматриваемая случайная величина, равно 5. Очевидно, что из всех указанных значений этому условию удовлетворяет только 1.Заметим, что вероятность того, что случайная величина
примет значения, не большие 10, равна 1. Таким образом, случайная величина может принимать значения только в диапазоне от 5 до 10. Поэтому она может принимать значения 6, 7 и 9.