График плотности распределения непрерывной случайной величины X имеет вид:
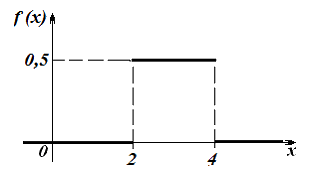
Тогда функция распределения непрерывной случайной величины X может иметь вид …
Тогда функция распределения непрерывной случайной величины X может иметь вид …
- ✓
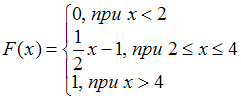
В соответствии с графиком, имеем: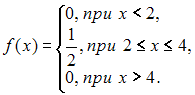 
Согласно определению, функция плотности распределения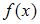
удовлетворяет условию 
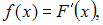где 
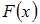– функция распределения случайной величины.
Рассмотрим, выполняется ли это условие для представленных в ответах функций распределения.
При дифференцировании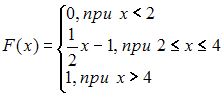
получим 
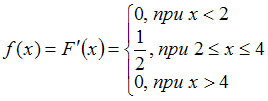, то есть эта функция распределения непрерывной случайной величины является искомой.
Для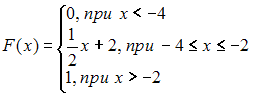
дифференцирование нецелесообразно, так как диапазоны значений переменной х не совпадают с теми, которые представлены на графике функции плотности распределения. Согласно графику, функция плотности распределения меняет свое значение в точках 
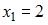и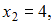 
а функция распределения, согласно алгебраической форме записи, меняет свой характер в точках 
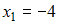и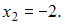 
При дифференцировании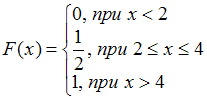
получим 
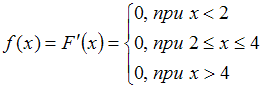, что не соответствует представленному графику плотности распределения.
Функция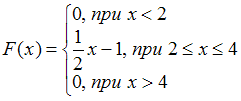
должна быть исключена из рассмотрения, так как не является функцией распределения непрерывной случайной величины (значение функции при неограниченном увеличении значения аргумента должно равняться 1).
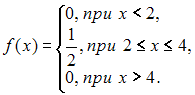
Согласно определению, функция плотности распределения
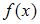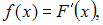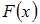удовлетворяет условию где – функция распределения случайной величины.Рассмотрим, выполняется ли это условие для представленных в ответах функций распределения.
При дифференцировании
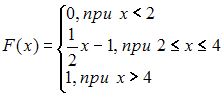получим 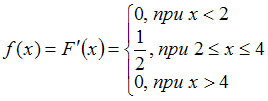, то есть эта функция распределения непрерывной случайной величины является искомой.Для
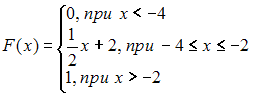дифференцирование нецелесообразно, так как диапазоны значений переменной х не совпадают с теми, которые представлены на графике функции плотности распределения. Согласно графику, функция плотности распределения меняет свое значение в точках 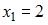и 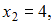а функция распределения, согласно алгебраической форме записи, меняет свой характер в точках 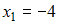и 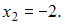При дифференцировании
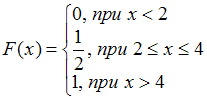получим 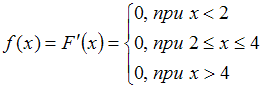, что не соответствует представленному графику плотности распределения.Функция
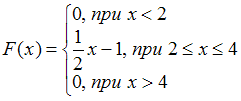должна быть исключена из рассмотрения, так как не является функцией распределения непрерывной случайной величины (значение функции при неограниченном увеличении значения аргумента должно равняться 1).