Математическое ожидание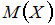 
случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью, равно …
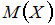случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью, равно …
- ✓ 4
Согласно определению, математическим ожиданием случайной величины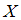 
с законом распределения
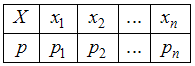
называется число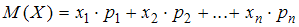
.
Составим закон распределения случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью (допустим,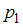
):
.
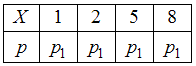Для определения значения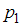
воспользуемся формулой: 
.
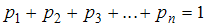В нашем случае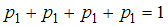
. Отсюда 
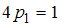, то есть 
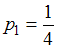. Таким образом, закон распределения случайной величины имеет вид:
.
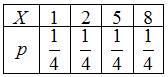Математическое ожидание случайной величины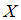
равно 
.
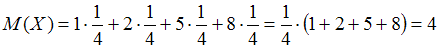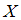с законом распределения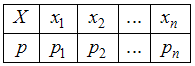называется число
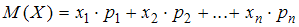.Составим закон распределения случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью (допустим,
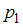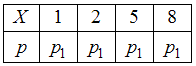):.Для определения значения
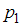воспользуемся формулой: 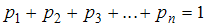.В нашем случае
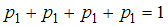. Отсюда 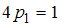, то есть 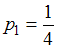. Таким образом, закон распределения случайной величины имеет вид: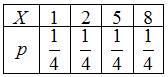.Математическое ожидание случайной величины
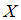равно 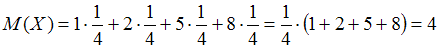.