 – множество двузначных чисел,
– множество двузначных чисел, 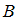 – множество чисел, кратных 3. Тогда для числа 35 верны следующие утверждения …
– множество чисел, кратных 3. Тогда для числа 35 верны следующие утверждения …
- ✓
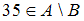
- ✓
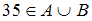
Разность множеств 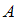 и
и 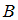 есть множество
есть множество 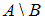 , состоящее из элементов множества
, состоящее из элементов множества 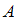 , не являющихся элементами множества
, не являющихся элементами множества 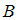 . Значит, в него войдут двузначные числа, не кратные 3. Число 35 является двузначным и не делится на 3, следовательно, высказывание
. Значит, в него войдут двузначные числа, не кратные 3. Число 35 является двузначным и не делится на 3, следовательно, высказывание 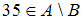 истинно.
истинно.
Пересечение множеств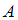 и
и 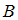 есть множество
есть множество 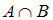 , состоящее из элементов, общих для обоих множеств. Значит, в него войдут двузначные числа, кратные 3. Число 35 является двузначным, но не делится на 3, следовательно, высказывание
, состоящее из элементов, общих для обоих множеств. Значит, в него войдут двузначные числа, кратные 3. Число 35 является двузначным, но не делится на 3, следовательно, высказывание 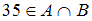 ложно.
ложно.
Объединение множеств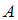 и
и 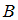 есть множество
есть множество 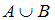 , состоящее из всех элементов этих множеств. Значит, в него войдут двузначные числа и числа, кратные 3. Число 35 является двузначным, следовательно, высказывание
, состоящее из всех элементов этих множеств. Значит, в него войдут двузначные числа и числа, кратные 3. Число 35 является двузначным, следовательно, высказывание 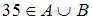 истинно.
истинно.
Разность множеств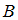 и
и 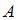 есть множество
есть множество 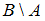 , состоящее из элементов множества
, состоящее из элементов множества 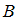 , не являющихся элементами множества
, не являющихся элементами множества 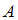 . Значит, в него войдут числа, кратные 3, не являющиеся двузначными. Число 35 не делится на 3, следовательно, высказывание
. Значит, в него войдут числа, кратные 3, не являющиеся двузначными. Число 35 не делится на 3, следовательно, высказывание 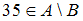 ложно.
ложно.
Таким образом, справедливы высказывания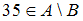 и
и 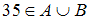 .
.
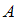 и
и 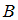 есть множество
есть множество 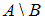 , состоящее из элементов множества
, состоящее из элементов множества 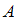 , не являющихся элементами множества
, не являющихся элементами множества 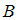 . Значит, в него войдут двузначные числа, не кратные 3. Число 35 является двузначным и не делится на 3, следовательно, высказывание
. Значит, в него войдут двузначные числа, не кратные 3. Число 35 является двузначным и не делится на 3, следовательно, высказывание 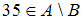 истинно.
истинно.Пересечение множеств
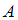 и
и 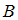 есть множество
есть множество 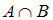 , состоящее из элементов, общих для обоих множеств. Значит, в него войдут двузначные числа, кратные 3. Число 35 является двузначным, но не делится на 3, следовательно, высказывание
, состоящее из элементов, общих для обоих множеств. Значит, в него войдут двузначные числа, кратные 3. Число 35 является двузначным, но не делится на 3, следовательно, высказывание 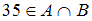 ложно.
ложно.Объединение множеств
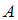 и
и 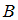 есть множество
есть множество 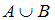 , состоящее из всех элементов этих множеств. Значит, в него войдут двузначные числа и числа, кратные 3. Число 35 является двузначным, следовательно, высказывание
, состоящее из всех элементов этих множеств. Значит, в него войдут двузначные числа и числа, кратные 3. Число 35 является двузначным, следовательно, высказывание 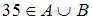 истинно.
истинно.Разность множеств
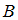 и
и 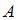 есть множество
есть множество 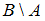 , состоящее из элементов множества
, состоящее из элементов множества 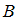 , не являющихся элементами множества
, не являющихся элементами множества 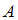 . Значит, в него войдут числа, кратные 3, не являющиеся двузначными. Число 35 не делится на 3, следовательно, высказывание
. Значит, в него войдут числа, кратные 3, не являющиеся двузначными. Число 35 не делится на 3, следовательно, высказывание 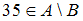 ложно.
ложно.Таким образом, справедливы высказывания
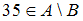 и
и 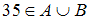 .
.