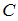– множество юношей студенческой группы, 
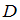– множество отличников этой группы. Известно, что 
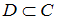, причем 
, 
, 
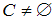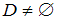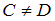. Тогда справедливы высказывания …
- ✓ «Все отличники группы являются юношами»
- ✓ «В группе есть отличники»
По условию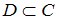 
, значит, все элементы множества 
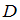являются элементами множества 
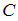. Так как 
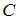– множество юношей студенческой группы, 
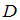– множество отличников этой группы, то это означает, что все отличники студенческой группы являются юношами. Следовательно, высказывание «Все отличники группы являются юношами» истинно. Так как 
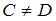, то высказывание «Все юноши группы являются отличниками» ложно.
По условию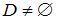
, значит, в группе есть отличники, и высказывание «В группе есть отличники» истинно.
Так как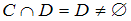
, то множества 
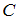и 
и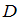меют общие элементы, значит, среди юношей есть отличники, и высказывание «Ни один юноша группы не является отличником» ложно.
Таким образом, верны высказывания «Все отличники группы являются юношами» и «В группе есть отличники».
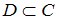, значит, все элементы множества 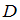являются элементами множества 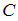. Так как 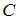– множество юношей студенческой группы, 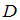– множество отличников этой группы, то это означает, что все отличники студенческой группы являются юношами. Следовательно, высказывание «Все отличники группы являются юношами» истинно. Так как 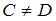, то высказывание «Все юноши группы являются отличниками» ложно.По условию
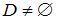, значит, в группе есть отличники, и высказывание «В группе есть отличники» истинно.Так как
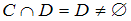, то множества 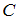и 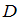имеют общие элементы, значит, среди юношей есть отличники, и высказывание «Ни один юноша группы не является отличником» ложно.Таким образом, верны высказывания «Все отличники группы являются юношами» и «В группе есть отличники».
