Пусть A – множество чисел, кратных 2; B – множество чисел, кратных 4; C – множество нечетных чисел. Тогда отношения между данными множествами верно изображены на диаграммах …
- ✓

- ✓

Множества 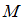 и
и 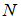 не пересекаются (
не пересекаются (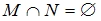 ), если они не имеют общих элементов. В этом случае на диаграмме фигуры, изображающие множества
), если они не имеют общих элементов. В этом случае на диаграмме фигуры, изображающие множества 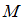 и
и 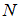 , не должны пересекаться.
, не должны пересекаться.
Множества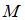 и
и 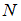 пересекаются (
пересекаются (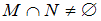 ), если они имеют общие элементы. В этом случае на диаграмме фигуры, изображающие множества
), если они имеют общие элементы. В этом случае на диаграмме фигуры, изображающие множества 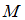 и
и 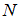 , должны пересекаться.
, должны пересекаться.
Множество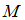 включено во множество
включено во множество 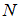 (
(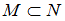 ), если каждый элемент множества
), если каждый элемент множества 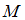 одновременно является элементом множества
одновременно является элементом множества 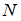 . В этом случае на диаграмме фигура, изображающая множество
. В этом случае на диаграмме фигура, изображающая множество 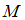 , должна находиться внутри фигуры, изображающей множество
, должна находиться внутри фигуры, изображающей множество 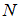 .
.
Определим, в каком отношении находятся множества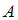 и
и 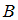 , если
, если 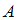 – множество чисел, кратных 2,
– множество чисел, кратных 2, 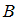 – множество чисел, кратных 4. Всякое число, делящееся на 4, делится на 2 (4, 8, 12, …). Следовательно, каждый элемент множества
– множество чисел, кратных 4. Всякое число, делящееся на 4, делится на 2 (4, 8, 12, …). Следовательно, каждый элемент множества 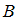 одновременно является элементом множества
одновременно является элементом множества 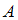 , то есть
, то есть 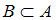 . Обратное же неверно: если число делится на 2, то оно не обязательно делится на 4 (например, 2, 6). Значит, на диаграмме фигура, изображающая множество
. Обратное же неверно: если число делится на 2, то оно не обязательно делится на 4 (например, 2, 6). Значит, на диаграмме фигура, изображающая множество 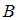 , должна находиться внутри фигуры, изображающей множество
, должна находиться внутри фигуры, изображающей множество 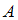 . Таким образом, диаграмма
. Таким образом, диаграмма

верно изображает множества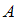 и
и 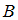 , а диаграмма
, а диаграмма

неверна.
Определим, в каком отношении находятся множества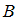 и
и 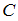 .
. 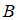 – множество чисел, кратных 4;
– множество чисел, кратных 4; 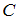 – множество нечетных чисел. Если число делится на 4, то оно делится и на 2, то есть является четным и не является нечетным. Значит, множества
– множество нечетных чисел. Если число делится на 4, то оно делится и на 2, то есть является четным и не является нечетным. Значит, множества 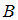 и
и 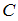 не имеют общих элементов, то есть не пересекаются,
не имеют общих элементов, то есть не пересекаются, 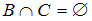 . Следовательно, на диаграмме фигуры, изображающие множества
. Следовательно, на диаграмме фигуры, изображающие множества 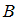 и
и 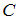 , не должны пересекаться, и диаграмма
, не должны пересекаться, и диаграмма

верно изображает множества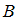 и
и 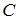 , а диаграмма
, а диаграмма

неверна.
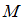 и
и 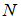 не пересекаются (
не пересекаются (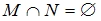 ), если они не имеют общих элементов. В этом случае на диаграмме фигуры, изображающие множества
), если они не имеют общих элементов. В этом случае на диаграмме фигуры, изображающие множества 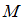 и
и 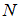 , не должны пересекаться.
, не должны пересекаться.Множества
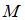 и
и 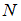 пересекаются (
пересекаются (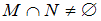 ), если они имеют общие элементы. В этом случае на диаграмме фигуры, изображающие множества
), если они имеют общие элементы. В этом случае на диаграмме фигуры, изображающие множества 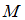 и
и 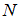 , должны пересекаться.
, должны пересекаться.Множество
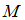 включено во множество
включено во множество 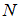 (
(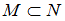 ), если каждый элемент множества
), если каждый элемент множества 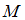 одновременно является элементом множества
одновременно является элементом множества 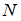 . В этом случае на диаграмме фигура, изображающая множество
. В этом случае на диаграмме фигура, изображающая множество 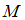 , должна находиться внутри фигуры, изображающей множество
, должна находиться внутри фигуры, изображающей множество 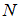 .
.Определим, в каком отношении находятся множества
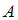 и
и 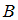 , если
, если 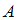 – множество чисел, кратных 2,
– множество чисел, кратных 2, 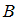 – множество чисел, кратных 4. Всякое число, делящееся на 4, делится на 2 (4, 8, 12, …). Следовательно, каждый элемент множества
– множество чисел, кратных 4. Всякое число, делящееся на 4, делится на 2 (4, 8, 12, …). Следовательно, каждый элемент множества 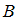 одновременно является элементом множества
одновременно является элементом множества 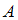 , то есть
, то есть 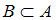 . Обратное же неверно: если число делится на 2, то оно не обязательно делится на 4 (например, 2, 6). Значит, на диаграмме фигура, изображающая множество
. Обратное же неверно: если число делится на 2, то оно не обязательно делится на 4 (например, 2, 6). Значит, на диаграмме фигура, изображающая множество 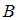 , должна находиться внутри фигуры, изображающей множество
, должна находиться внутри фигуры, изображающей множество 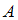 . Таким образом, диаграмма
. Таким образом, диаграмма
верно изображает множества
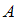 и
и 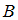 , а диаграмма
, а диаграмма
неверна.
Определим, в каком отношении находятся множества
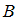 и
и 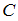 .
. 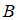 – множество чисел, кратных 4;
– множество чисел, кратных 4; 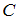 – множество нечетных чисел. Если число делится на 4, то оно делится и на 2, то есть является четным и не является нечетным. Значит, множества
– множество нечетных чисел. Если число делится на 4, то оно делится и на 2, то есть является четным и не является нечетным. Значит, множества 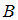 и
и 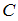 не имеют общих элементов, то есть не пересекаются,
не имеют общих элементов, то есть не пересекаются, 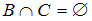 . Следовательно, на диаграмме фигуры, изображающие множества
. Следовательно, на диаграмме фигуры, изображающие множества 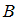 и
и 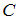 , не должны пересекаться, и диаграмма
, не должны пересекаться, и диаграмма
верно изображает множества
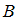 и
и 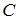 , а диаграмма
, а диаграмма
неверна.
