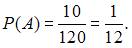Абонент получил 10 SMS сообщений, половину из которых прочел. Вероятность того, что при случайном выборе 3 сообщений из общего списка все три не были прочитаны ранее, равна …
✓ 
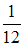
Решение:
Вероятностью события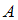
называется отношение числа элементарных исходов 
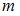, благоприятствующих данному событию, к числу 
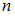равновозможных элементарных исходов испытания: 
.
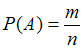Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов испытания.
Испытание состоит в том, что случайным образом выбираются 3 сообщения из 10 имеющихся. Общее число элементарных исходов определим, используя формулу для нахождения числа сочетаний из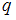
элементов по 
: 
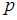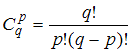. Выясним, сколько существует способов выбора 3 сообщений (
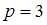) из 10 имеющихся (
).
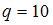Имеем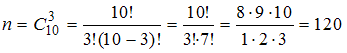
.
Событие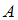
состоит в том, что все 3 сообщения не были прочитаны ранее. Общее число непрочитанных сообщений составляет половину от 10, то есть 5 сообщений. Поэтому число исходов, благоприятствующих событию 
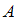, определяется как количество способов, которыми можно выбрать 3 сообщения из 5: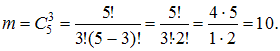 
Следовательно, вероятность события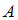
равна 
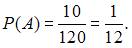
Вероятностью события
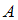называется отношение числа элементарных исходов 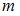, благоприятствующих данному событию, к числу 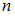равновозможных элементарных исходов испытания: 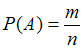.Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов испытания.
Испытание состоит в том, что случайным образом выбираются 3 сообщения из 10 имеющихся. Общее число элементарных исходов определим, используя формулу для нахождения числа сочетаний из
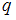элементов по 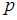: 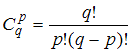. Выясним, сколько существует способов выбора 3 сообщений (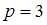) из 10 имеющихся (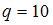).Имеем
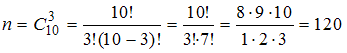.Событие
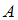состоит в том, что все 3 сообщения не были прочитаны ранее. Общее число непрочитанных сообщений составляет половину от 10, то есть 5 сообщений. Поэтому число исходов, благоприятствующих событию 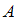, определяется как количество способов, которыми можно выбрать 3 сообщения из 5: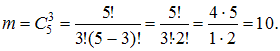 Следовательно, вероятность события
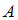равна 