Дан доверительный интервал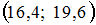 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
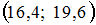для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
✓ 
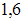
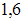
Решение:
Точность интервальной оценки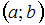
определяется как 
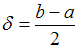, то есть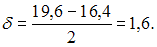 
Точность интервальной оценки
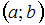определяется как 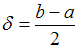, то есть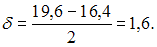 [/paid_content]
