Дано статическое распределение выборки объемом 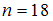 :
:
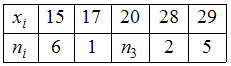 .
.
Тогда мода выборки равна …
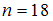 :
: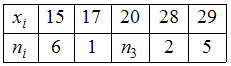 .
.Тогда мода выборки равна …
✓ 15
Решение:
Модой называется варианта, имеющая наибольшую частоту. Но частота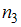 неизвестна. Найдем ее значение.
неизвестна. Найдем ее значение.
Наблюдаемые значения рассматриваемого признака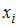 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота  . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 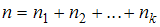 , где
, где  – количество вариант.
– количество вариант.
Статистическим распределением выборки называют перечень вариант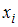 и соответствующих им частот
и соответствующих им частот 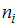 , который записывается в виде таблицы:
, который записывается в виде таблицы: 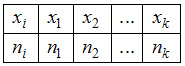 .
.
Объем данной выборки, представленной статистическим распределением, . Отсюда
. Отсюда  . Тогда статистическое распределение имеет вид:
. Тогда статистическое распределение имеет вид:
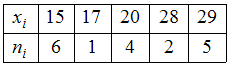 , то есть
, то есть
варианта 15 имеет частоту 6,
варианта 17 имеет частоту 1,
варианта 20 имеет частоту 4,
варианта 28 имеет частоту 2,
варианта 29 имеет частоту 5.
Таким образом, наибольшую частоту, равную 6, имеет варианта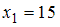 . Мода выборки, представленной статистическим распределением, равна 15.
. Мода выборки, представленной статистическим распределением, равна 15.
Модой называется варианта, имеющая наибольшую частоту. Но частота
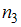 неизвестна. Найдем ее значение.
неизвестна. Найдем ее значение.Наблюдаемые значения рассматриваемого признака
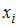 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота  . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 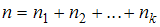 , где
, где  – количество вариант.
– количество вариант. Статистическим распределением выборки называют перечень вариант
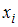 и соответствующих им частот
и соответствующих им частот 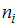 , который записывается в виде таблицы:
, который записывается в виде таблицы: 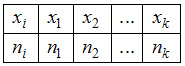 .
.Объем данной выборки, представленной статистическим распределением,
 . Отсюда
. Отсюда  . Тогда статистическое распределение имеет вид:
. Тогда статистическое распределение имеет вид: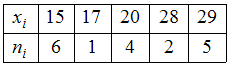 , то есть
, то естьварианта 15 имеет частоту 6,
варианта 17 имеет частоту 1,
варианта 20 имеет частоту 4,
варианта 28 имеет частоту 2,
варианта 29 имеет частоту 5.
Таким образом, наибольшую частоту, равную 6, имеет варианта
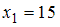 . Мода выборки, представленной статистическим распределением, равна 15.
. Мода выборки, представленной статистическим распределением, равна 15.