Даны множества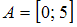 
– отрезок числовой оси и 
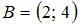– интервал числовой оси. Тогда для них истинны высказывания …
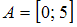– отрезок числовой оси и 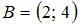– интервал числовой оси. Тогда для них истинны высказывания …
- ✓
- ✓
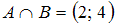
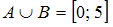
Решение:
Найдем пересечение и объединение множеств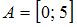
и 
.
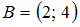Отрезок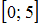
представляет собой часть числовой оси от точки 
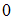до точки 
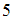, включая точк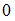и 
и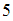 
. Интервал 
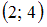– это часть числовой оси от точки 
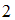до точки 
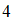, не включающая точк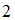и 
и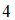 
. Изобразим эти множества на рисунке:
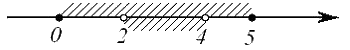
Пересечение множеств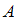
и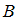 
есть множество, состоящее из элементов, общих для обоих множеств. В нашем случае в него войдут точки числовой оси, принадлежащие одновременно и интервалу 
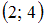, и отрезку 
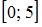, то есть все точки интервала 
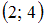. Таким образом, 
.
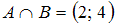Объединение множеств
и 
есть множество, состоящее из всех элементов этих множеств. В нашем случае в него войдут все точки числовой оси, принадлежащие интервалу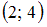 
и отрезку 
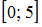, то есть все точки отрезка 
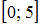. Таким образом, 
.
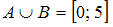Значит, истинны высказывания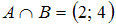
и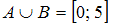 
.
Найдем пересечение и объединение множеств
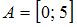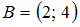и .Отрезок
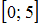представляет собой часть числовой оси от точки 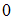до точки 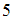, включая точк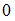и и 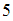. Интервал 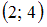– это часть числовой оси от точки 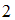до точки 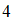, не включающая точк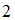и и 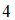. Изобразим эти множества на рисунке: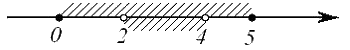Пересечение множеств
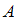и 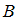есть множество, состоящее из элементов, общих для обоих множеств. В нашем случае в него войдут точки числовой оси, принадлежащие одновременно и интервалу 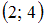, и отрезку 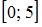, то есть все точки интервала 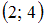. Таким образом, 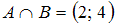. Объединение множеств
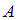и 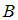есть множество, состоящее из всех элементов этих множеств. В нашем случае в него войдут все точки числовой оси, принадлежащие интервалу 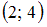и отрезку 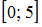, то есть все точки отрезка 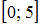. Таким образом, 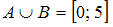.Значит, истинны высказывания
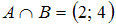и 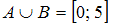.