Для функции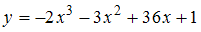 
точка максимума 
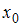принимает значение, равное …
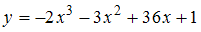точка максимума 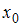принимает значение, равное …
✓ 
Решение:
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует.
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим:
Последнее уравнение имеет корни:
Отметим найденные значения на числовой прямой. Найдем знак производной 
на каждом из получившихся промежутков.
Точки
и 
являются экстремальными, так как при переходе через эти точки производная меняет знак. 
– точка максимума, так как производная меняет знак с «+» на «
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует.
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим:
Последнее уравнение имеет корни:
Отметим найденные значения на числовой прямой. Найдем знак производной на каждом из получившихся промежутков.Точки
и являются экстремальными, так как при переходе через эти точки производная меняет знак. – точка максимума, так как производная меняет знак с «+» на «[/paid_content]
