Для исследования числового ряда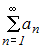 
на сходимость можно пользоваться признаком Даламбера
и признаком Коши 
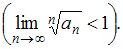
Тогда сходящимися являются ряды …
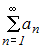на сходимость можно пользоваться признаком Даламбера и признаком Коши 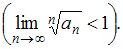Тогда сходящимися являются ряды …
- ✓
- ✓
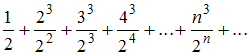
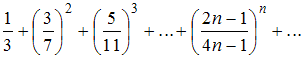
Решение:
1) Для ряда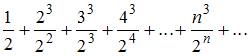
воспользуемся признаком Даламбера.
Имеем: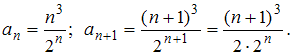
Тогда получим: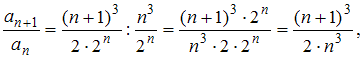
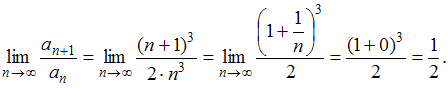
Так как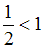
, то данный ряд сходится.
2) Для ряда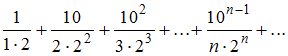
воспользуемся признаком Даламбера.
Имеем: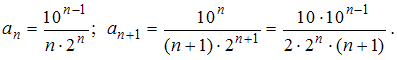
Тогда получим: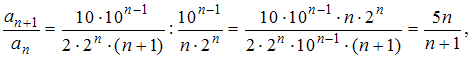
.
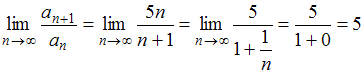Так как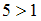
, то данный ряд расходится.
3) Для ряда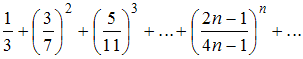
воспользуемся признаком Коши.
Имеем: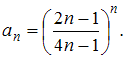
Тогда получим: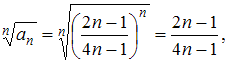 
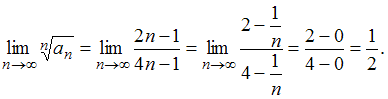
Так как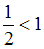
, то данный ряд сходится.
4) Для ряда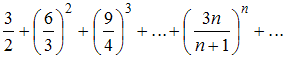
воспользуемся признаком Коши.
Имеем: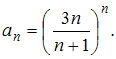
Тогда получим: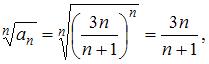 
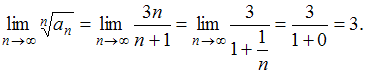
Так как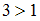
, то данный ряд расходится.
1) Для ряда
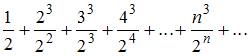воспользуемся признаком Даламбера.Имеем:
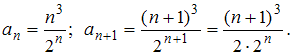
Тогда получим:
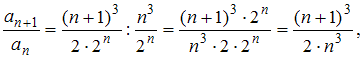
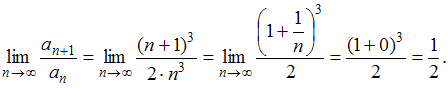
Так как
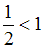, то данный ряд сходится.2) Для ряда
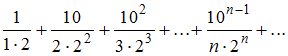воспользуемся признаком Даламбера.Имеем:
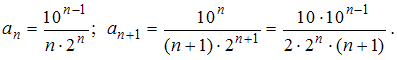
Тогда получим:
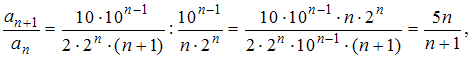
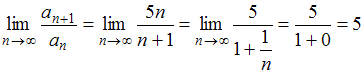.Так как
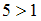, то данный ряд расходится.3) Для ряда
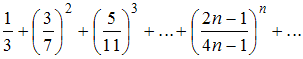воспользуемся признаком Коши.Имеем:
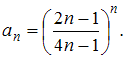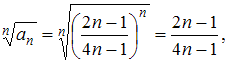
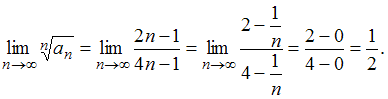
Тогда получим: Так как
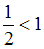, то данный ряд сходится.4) Для ряда
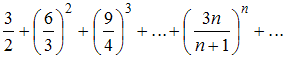воспользуемся признаком Коши.Имеем:
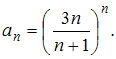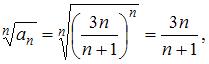
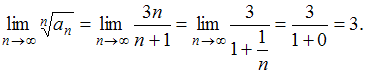
Тогда получим: Так как
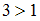, то данный ряд расходится.[/paid_content]
