Для оценки с надежностью  математического ожидания
математического ожидания  нормально распределенного признака
нормально распределенного признака  по выборочной средней
по выборочной средней 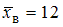 при среднем квадратичном отклонении
при среднем квадратичном отклонении 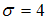 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 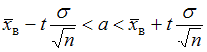 , где
, где  – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 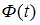 , при котором
, при котором  ,
, 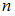 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для 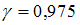 равно
равно 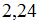 .
.
Установите соответствие между объемами выборок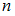 и соответствующим доверительными интервалами.
и соответствующим доверительными интервалами.
1.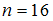
2.
 математического ожидания
математического ожидания  нормально распределенного признака
нормально распределенного признака  по выборочной средней
по выборочной средней 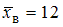 при среднем квадратичном отклонении
при среднем квадратичном отклонении 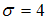 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 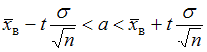 , где
, где  – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 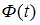 , при котором
, при котором  ,
, 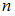 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для 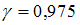 равно
равно 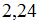 .
.Установите соответствие между объемами выборок
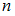 и соответствующим доверительными интервалами.
и соответствующим доверительными интервалами.1.
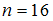
2.

✓ 15
Решение:
Требуется найти доверительный интервал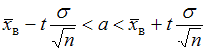 . Известно, что
. Известно, что 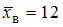 ,
, 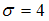 и
и 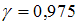 (
(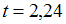 ).
).
Если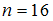 , то
, то 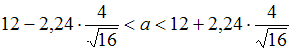 . Следовательно,
. Следовательно, 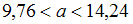 .
.
Если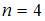 , то
, то 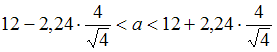 . Следовательно,
. Следовательно, 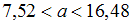 .
.
Требуется найти доверительный интервал
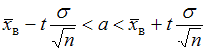 . Известно, что
. Известно, что 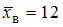 ,
, 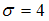 и
и 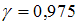 (
(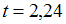 ).
).Если
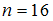 , то
, то 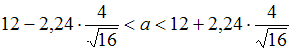 . Следовательно,
. Следовательно, 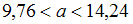 .
.Если
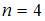 , то
, то 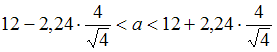 . Следовательно,
. Следовательно, 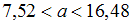 .
.