Для оценки с надежностью 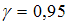 математического ожидания
математического ожидания 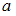 нормально распределенного признака
нормально распределенного признака 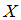 по выборочной средней
по выборочной средней 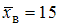 при среднем квадратичном отклонении
при среднем квадратичном отклонении  генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 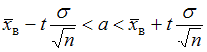 , где
, где 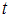 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 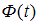 , при котором
, при котором 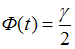 ,
, 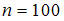 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для  равно
равно 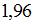 .
.
Установите соответствие между доверительными интервалами и средними квадратичными отклонениями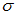 , по которым они получены:
, по которым они получены:
1)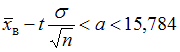 ,
,
2)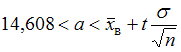 .
.
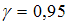 математического ожидания
математического ожидания 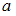 нормально распределенного признака
нормально распределенного признака 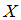 по выборочной средней
по выборочной средней 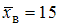 при среднем квадратичном отклонении
при среднем квадратичном отклонении  генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 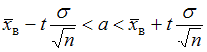 , где
, где 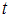 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 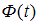 , при котором
, при котором 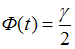 ,
, 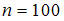 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для  равно
равно 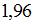 .
.Установите соответствие между доверительными интервалами и средними квадратичными отклонениями
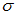 , по которым они получены:
, по которым они получены:1)
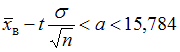 ,
,2)
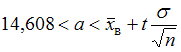 .
.
- ✓
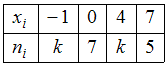
- ✓
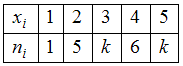
Решение:
Дан доверительный интервал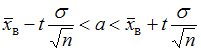 . Согласно условию,
. Согласно условию, 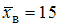 ,
, 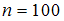 ,
, 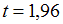 . Таким образом,
. Таким образом, 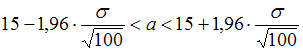 или
или 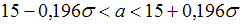 .
.
В случае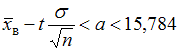 имеем
имеем 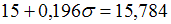 . Отсюда
. Отсюда 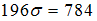 , то есть
, то есть 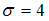 .
.
В случае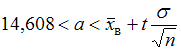 имеем
имеем 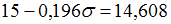 . Отсюда
. Отсюда 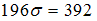 , то есть
, то есть 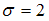 .
.
Дан доверительный интервал
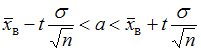 . Согласно условию,
. Согласно условию, 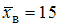 ,
, 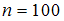 ,
, 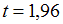 . Таким образом,
. Таким образом, 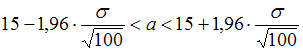 или
или 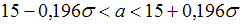 .
.В случае
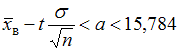 имеем
имеем 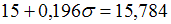 . Отсюда
. Отсюда 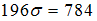 , то есть
, то есть 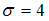 .
.В случае
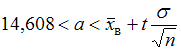 имеем
имеем 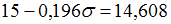 . Отсюда
. Отсюда 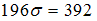 , то есть
, то есть 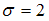 .
.