Для оценки с некоторой надежностью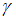 
математического ожидания a нормально распределенного признака X по выборочной средней 
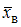при среднем квадратичном отклонении 
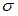генеральной совокупности использовали доверительный интервал 
где t – значение аргумента функции Лапласа 
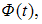при котором 
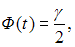n – объем выборки.
Установите соответствие между значениями
и возможными соответствующими доверительными интервалами:
1)
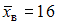
2)
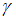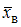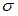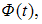математического ожидания a нормально распределенного признака X по выборочной средней при среднем квадратичном отклонении генеральной совокупности использовали доверительный интервал где t – значение аргумента функции Лапласа при котором 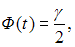n – объем выборки.Установите соответствие между значениями
и возможными соответствующими доверительными интервалами:1)
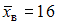
2)
✓ «Поверхность»
Решение:
Рассмотрим доверительный интервал
. Очевидно, что он симметричен относительно 
. Поэтому значение 
представляет собой середину доверительного интервала.
Кроме того, значение
может быть найдено как среднее арифметическое чисел, служащих границами интервала:
Если
то 
Если
то 
Заметим, что при
имеем 
Рассмотрим доверительный интервал
. Очевидно, что он симметричен относительно . Поэтому значение представляет собой середину доверительного интервала.Кроме того, значение
может быть найдено как среднее арифметическое чисел, служащих границами интервала:Если
то Если
то Заметим, что при
имеем 