Двое преподавателей принимают отчеты по лабораторным работам у десяти студентов. Вероятность получить зачет у первого преподавателя составляет 0,8, а у второго – 0,7. Первый преподаватель принимает k случайно выбранных студентов из 10, а остальные сдают отчеты второму преподавателю.
Установите соответствие между значением k и вероятностью сдать отчет для случайно выбранного студента.
1.
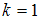
2.
Установите соответствие между значением k и вероятностью сдать отчет для случайно выбранного студента.
1.
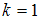
2.
✓ Шеф! Все пропало! Гипс снимают!
Решение:
Рассмотрим событие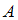
– случайно выбранный студент сдаст отчет. Оно может произойти при сдаче отчета как первому преподавателю (событие 
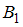), так и второму (событие 
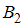). Заметим, что события 
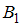и 
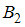несовместны, поскольку студент не может сдавать зачет сразу двум преподавателям, и противоположны, так как других вариантов для сдачи отчета у студентов нет. Поэтому вероятность события 
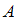может быть определена при помощи формулы полной вероятности: 
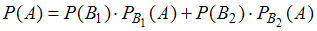, где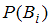 
– вероятность события 
; 
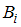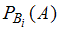– условная вероятность события 
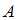, то есть вероятность события 
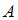, вычисленная в предположении, что событие 
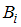наступило.
Событие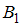
в данном случае состоит в том, что отчет принимает первый преподаватель. Тогда, согласно условию, 
.
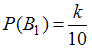Событие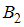
состоит в том, что отчет принимает второй преподаватель. Так как события 
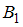и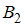 
являются противоположными, то 
.
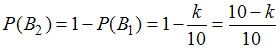Так как вероятность получить зачет у первого преподавателя составляет 0,8, а у второго – 0,7, то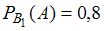
, 
.
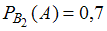Рассчитаем вероятности событий
и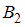 
:
при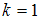
:
, 
,
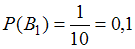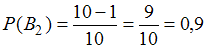при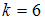
:
, 
.
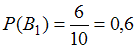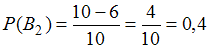Подставив полученные значения в формулу полной вероятности, имеем
при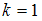
:
,
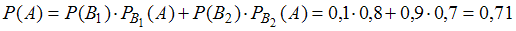при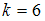
:
.
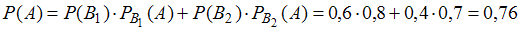Рассмотрим событие
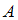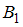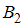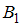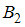– случайно выбранный студент сдаст отчет. Оно может произойти при сдаче отчета как первому преподавателю (событие ), так и второму (событие ). Заметим, что события и несовместны, поскольку студент не может сдавать зачет сразу двум преподавателям, и противоположны, так как других вариантов для сдачи отчета у студентов нет. Поэтому вероятность события 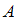может быть определена при помощи формулы полной вероятности: 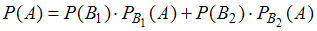, где 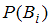– вероятность события 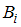; 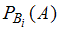– условная вероятность события 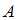, то есть вероятность события 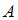, вычисленная в предположении, что событие 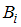наступило.Событие
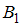в данном случае состоит в том, что отчет принимает первый преподаватель. Тогда, согласно условию, 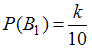.Событие
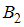состоит в том, что отчет принимает второй преподаватель. Так как события 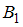и 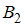являются противоположными, то 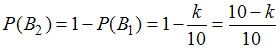.Так как вероятность получить зачет у первого преподавателя составляет 0,8, а у второго – 0,7, то
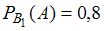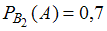, .Рассчитаем вероятности событи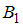й
и 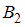:при
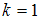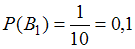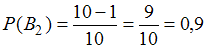:, ,при
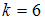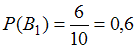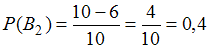:, .Подставив полученные значения в формулу полной вероятности, имеем
при
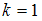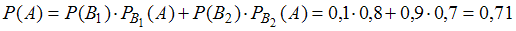:,при
:.
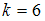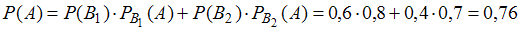