Фирма планирует организовать выпуск трех типов изделий: А, В и C.
Для производства любого изделия требуется затратить материалы двух видов:
I и II. Запасы материалов ограничены: вида I – 700 кг; вида II – 900 кг.
Для изготовления одного изделия типа A требуется 1 кг материалов вида I и 4 кг материалов вида II; для производства одного изделия типа В – 3 кг и 1 кг материалов видов I и II соответственно; для производства одного
изделия типа C – 1 кг и 3 кг материалов видов I и II соответственно. Прибыль от реализации одного изделия типа А составляет 2000 рублей, изделия типа В – 1800 рублей и изделия типа С – 1500 рублей. Требуется составить такой план производства изделий типов A, B и C, чтобы прибыль от реализации была наибольшей.
Пусть выпущено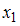
изделий типа A, 
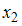изделий типа B и 
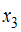изделий типа C.
Тогда математическая модель задачи будет иметь вид …
Для производства любого изделия требуется затратить материалы двух видов:
I и II. Запасы материалов ограничены: вида I – 700 кг; вида II – 900 кг.
Для изготовления одного изделия типа A требуется 1 кг материалов вида I и 4 кг материалов вида II; для производства одного изделия типа В – 3 кг и 1 кг материалов видов I и II соответственно; для производства одного
изделия типа C – 1 кг и 3 кг материалов видов I и II соответственно. Прибыль от реализации одного изделия типа А составляет 2000 рублей, изделия типа В – 1800 рублей и изделия типа С – 1500 рублей. Требуется составить такой план производства изделий типов A, B и C, чтобы прибыль от реализации была наибольшей.
Пусть выпущено
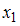изделий типа A, 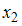изделий типа B и 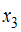изделий типа C.Тогда математическая модель задачи будет иметь вид …
✓ 
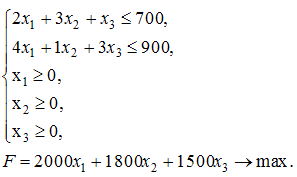
Решение:
Обращаем внимание, что два первых неравенства системы описывают ограничения на запасы материалов для изготовления изделий. Три последних должны указывать на то, что количество изделий не может быть отрицательным числом. Напоминаем, что в задаче требуется найти максимум.
Обращаем внимание, что два первых неравенства системы описывают ограничения на запасы материалов для изготовления изделий. Три последних должны указывать на то, что количество изделий не может быть отрицательным числом. Напоминаем, что в задаче требуется найти максимум.
[/paid_content]
