Линейное дифференциальное уравнение можно решить с помощью подстановки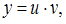 
где функция 
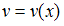подбирается так, чтобы после подстановки получилось уравнение с разделяющимися переменными.
Общим решением уравнения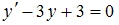
является …
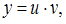где функция 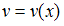подбирается так, чтобы после подстановки получилось уравнение с разделяющимися переменными.Общим решением уравнения
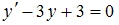является …
✓ 
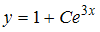
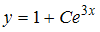
Решение:
Сделаем подстановку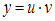
, тогда 
.
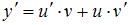Подставим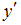
в исходное уравнение, получим: 
.
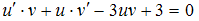Вынесем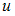
за скобки: 
.
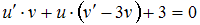В силу произвольности выбора функции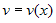
найдем ее из условия 
.
Тогда: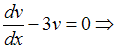
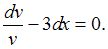
Проинтегрируем обе части уравнения: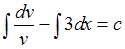
.
Считая, что
получим 
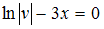, откуда 
.
Осталось решить уравнение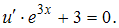
Имеем: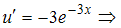
.
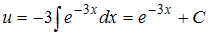Окончательно получим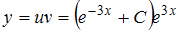
или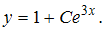 
Сделаем подстановку
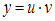, тогда 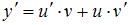.Подставим
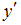в исходное уравнение, получим: 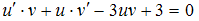.Вынесем
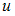за скобки: 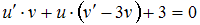.В силу произвольности выбора функции
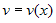найдем ее из условия .Тогда:
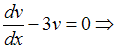
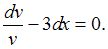
Проинтегрируем обе части уравнения:
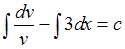.Считая, что
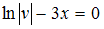получим , откуда .Осталось решить уравнение
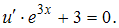
Имеем:
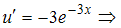
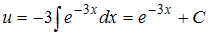.Окончательно получим
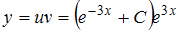или 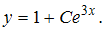[/paid_content]
