Математическое ожидание квадрата дискретной положительной случайной величины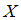 
равно 
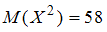, а ее среднее квадратичное отклонение 
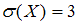. Тогда математическое ожидание, вычисленное при помощи формулы для расчета дисперсии 
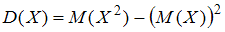, равно …
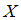равно 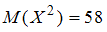, а ее среднее квадратичное отклонение 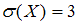. Тогда математическое ожидание, вычисленное при помощи формулы для расчета дисперсии 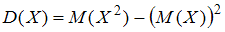, равно …
✓ 7
Решение:
Дисперсию случайной величины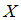
можно вычислить при помощи формулы, указанной в условии: 
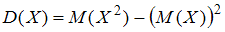. С другой стороны, средним квадратичным отклонением случайной величины называют квадратный корень из дисперсии: 
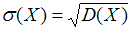. Поэтому 
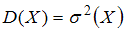. Подставив указанное выражение в первую формулу, получим: 
.
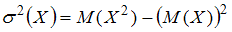Согласно условию,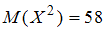
, 
.
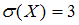Отсюда имеем: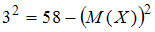
. Решая, получим 
.
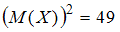В итоге математическое ожидание может принимать значения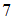
или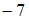 
. Учитывая, что рассматривается случайная величина, принимающая только положительные значения, заключаем, что математическое ожидание также величина положительная.
Таким образом, искомое значение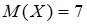
.
Дисперсию случайной величины
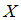можно вычислить при помощи формулы, указанной в условии: 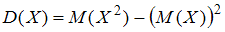. С другой стороны, средним квадратичным отклонением случайной величины называют квадратный корень из дисперсии: 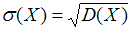. Поэтому 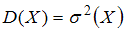. Подставив указанное выражение в первую формулу, получим: 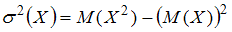.Согласно условию,
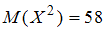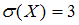, .Отсюда имеем:
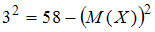. Решая, получим 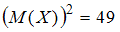.В итоге математическое ожидание может принимать значения
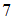или 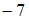. Учитывая, что рассматривается случайная величина, принимающая только положительные значения, заключаем, что математическое ожидание также величина положительная.Таким образом, искомое значение
.
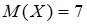