Медиана выборки объемом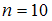 
, имеющей статистическое распределение
,
равна …
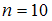, имеющей статистическое распределение,равна …
✓ 3
Решение:
Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака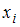
называются вариантами. Количество наблюдений данной варианты – частота 
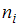. Число объектов выборочной совокупности называется объемом выборки 
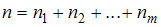, где 
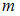– количество вариант. Если объем выборки 
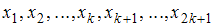– нечетное число, то есть 
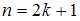, то медианой является варианта 
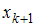; если объем выборки 
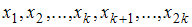– четное число, то есть 
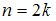, медиана равна 
.
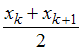Объем данной выборки, представленной статистическим распределением,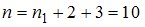
. Это число четное, поэтому 
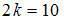, отсюда 
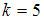, медиана равна 
.
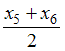Из соотношения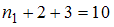
находим 
.
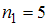Распределение примет вид:
.
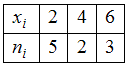Таким образом,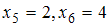
, поэтому медиана равна 
.
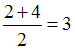Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака
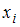называются вариантами. Количество наблюдений данной варианты – частота 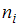. Число объектов выборочной совокупности называется объемом выборки 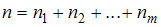, где 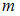– количество вариант. Если объем выборки 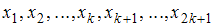– нечетное число, то есть 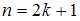, то медианой является варианта 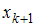; если объем выборки 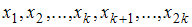– четное число, то есть 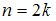, медиана равна 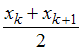.Объем данной выборки, представленной статистическим распределением,
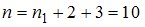. Это число четное, поэтому 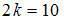, отсюда 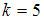, медиана равна 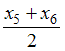.Из соотношения
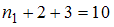находим 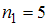. Распределение примет вид:
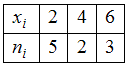.Таким образом,
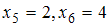, поэтому медиана равна .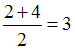