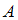– множество двузначных чисел, сумма цифр которых равна 5, 
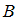– множество чисел, сумма цифр которых равна 5. Тогда для этих множеств справедливы высказывания:
- ✓ «Множество
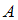конечно» - ✓ «Множество
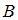бесконечно»
Решение:
Множество конечно, если оно состоит из конечного числа элементов.
Определим, конечны или бесконечны данные множества.
– множество двузначных чисел, сумма цифр которых равна 5. В это множество войдут двузначные числа 50, 41, 32, 23, 14, то есть 
. Множество 
состоит из 5 элементов, значит, оно конечно.
– множество чисел, сумма цифр которых равна 5. В это множество войдут однозначные или многозначные числа, сумма цифр которых равна 5: 5, 50, 41, 32, 23, 14, 500, 410, 401, 320, …, 5000, …, 50000, …, то есть данное множество бесконечно.
Таким образом, справедливы высказывания: «Множество
конечно» и «Множество 
бесконечно».
Множество конечно, если оно состоит из конечного числа элементов.
Определим, конечны или бесконечны данные множества.
– множество двузначных чисел, сумма цифр которых равна 5. В это множество войдут двузначные числа 50, 41, 32, 23, 14, то есть . Множество состоит из 5 элементов, значит, оно конечно. – множество чисел, сумма цифр которых равна 5. В это множество войдут однозначные или многозначные числа, сумма цифр которых равна 5: 5, 50, 41, 32, 23, 14, 500, 410, 401, 320, …, 5000, …, 50000, …, то есть данное множество бесконечно.Таким образом, справедливы высказывания: «Множество
конечно» и «Множество бесконечно».