Неопределенный интеграл 
равен …
равен …
✓ 
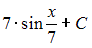
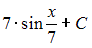
Решение:
Обращаем внимание, что подстановка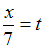
приводит рассматриваемый интеграл к табличному: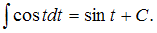 
Найдем дифференциал от обеих частей подстановки: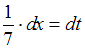
, тогда 
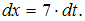Подставим получившиеся выражения в исходный интеграл:
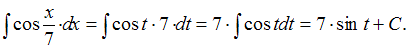
Заменив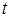
его выражением из подстановки, получим:
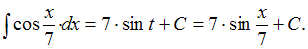
Обращаем внимание, что подстановка
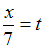приводит рассматриваемый интеграл к табличному: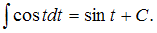 Найдем дифференциал от обеих частей подстановки:
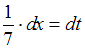, тогда 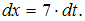Подставим получившиеся выражения в исходный интеграл: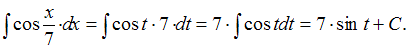Заменив
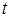его выражением из подстановки, получим: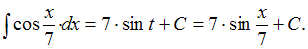[/paid_content]
