Определенный интеграл от любых непрерывных на отрезке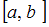 
функций 
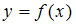и 
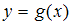не обладает свойством …
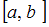функци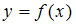й и 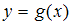не обладает свойством …
✓ 
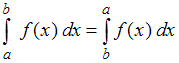
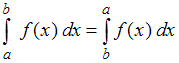
Решение:
Рассмотрим, какими из перечисленных свойств обладает определенный интеграл.
Мы знаем, что определенный интеграл обладает линейными свойствами, то есть: 1) постоянный множитель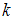
можно выносить за знак определенного интеграла 
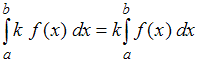и 2) интеграл алгебраической суммы равен сумме интегралов 
.
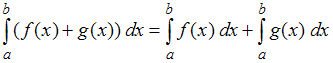Также для определенного интеграла справедливо свойство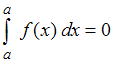
.
Но если в определенном интеграле поменять местами пределы интегрирования, то интеграл меняет знак: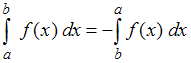
.
Следовательно, определенный интеграл не обладает свойством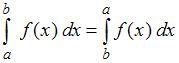
.
Рассмотрим, какими из перечисленных свойств обладает определенный интеграл.
Мы знаем, что определенный интеграл обладает линейными свойствами, то есть: 1) постоянный множитель
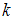можно выносить за знак определенного интеграла 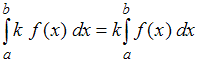и 2) интеграл алгебраической суммы равен сумме интегралов 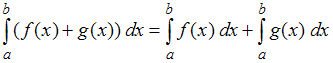.Также для определенного интеграла справедливо свойство
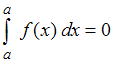.Но если в определенном интеграле поменять местами пределы интегрирования, то интеграл меняет знак:
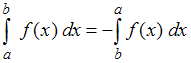.Следовательно, определенный интеграл не обладает свойством
.
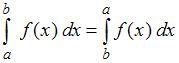