По двум независимым выборкам, объемы которых 
, 
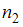, извлеченным из нормальных совокупностей 
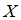и 
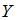, найдены исправленные выборочные дисперси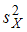и 
и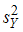 
. Надо проверить нулевую гипотезу 
: 
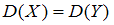о равенстве генеральных дисперсий, при конкурирующей гипотезе 
: 
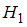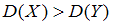. Для этого надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 
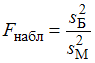и сравнить с критической точкой 
. Если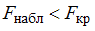 
– нет основания отвергнуть нулевую гипотезу. Если 
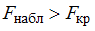– нулевую гипотезу отвергают.
Известно, что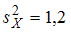
и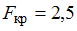 
. Тогда значение дисперсии 
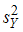, при котором нулевую гипотезу отвергают, равно …
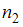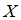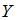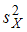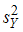, , извлеченным из нормальных совокупностей и , найдены исправленные выборочные дисперсии и . Надо проверить нулевую гипотезу : 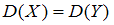о равенстве генеральных дисперсий, при конкурирующей гипотезе 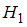: 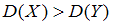. Для этого надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 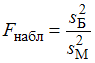и сравнить с критической точкой . Если 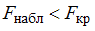– нет основания отвергнуть нулевую гипотезу. Если 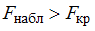– нулевую гипотезу отвергают.Известно, что
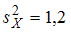и 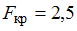. Тогда значение дисперсии 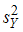, при котором нулевую гипотезу отвергают, равно …
✓ 3,6
Решение:
В условии задачи приведено правило, которое используется для проверки нулевой гипотезы
: 
о равенстве генеральных дисперсий, при конкурирующей гипотезе 
: 
. Согласно этому правилу, надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 
и сравнить с критической точкой 
. Если 
– нет основания отвергнуть нулевую гипотезу. Если 
– нулевую гипотезу отвергают.
Итак, для решения задачи найдем наблюдаемое значение критерия
.
Рассмотрим данные дисперсии.
Если
и 
, то 
. Заметим, что 
. В данном случае 
. Следовательно, 
отвергают.
Если
и 
, то 
. Заметим, что 
. В данном случае 
. Следовательно, нет основания отвергнуть нулевую гипотезу.
Если
и 
, то 
. Заметим, что 
. В данном случае 
. Следовательно, нет основания отвергнуть нулевую гипотезу.
Если
и 
, то 
. Заметим, что 
. В данном случае 
. Следовательно, нет основания отвергнуть нулевую гипотезу.
Следовательно, значение дисперсии
, при котором нулевую гипотезу отвергают, равно 3,6.
В условии задачи приведено правило, которое используется для проверки нулевой гипотезы
: о равенстве генеральных дисперсий, при конкурирующей гипотезе : . Согласно этому правилу, надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) и сравнить с критической точкой . Если – нет основания отвергнуть нулевую гипотезу. Если – нулевую гипотезу отвергают.Итак, для решения задачи найдем наблюдаемое значение критерия
.Рассмотрим данные дисперсии.
Если
и , то . Заметим, что . В данном случае . Следовательно, отвергают.Если
и , то . Заметим, что . В данном случае . Следовательно, нет основания отвергнуть нулевую гипотезу.Если
и , то . Заметим, что . В данном случае . Следовательно, нет основания отвергнуть нулевую гипотезу.Если
и , то . Заметим, что . В данном случае . Следовательно, нет основания отвергнуть нулевую гипотезу.Следовательно, значение дисперсии
, при котором нулевую гипотезу отвергают, равно 3,6.