При сравнении двух дисперсий нормальных генеральных совокупностей наблюдаемое значение критерия находится по таблице критических точек распределения …
✓ Фишера–Снедекора
Решение:
Напомним правило, по которому проверяется гипотеза о равенстве генеральных дисперсий нормальных совокупностей.
Пусть по независимым выборкам, объемы которых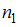
и 
, и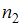звлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперси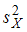и 
и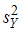 
. Требуется сравнить эти дисперсии.
Напомним одно из правил, по которому проверяется гипотеза о равенстве генеральных дисперсий нормальных совокупностей:
Для того чтобы при заданном уровне значимости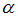
проверить нулевую гипотезу 
: 
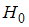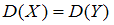о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе 
: 
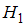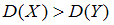, надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 
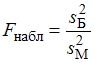и по таблице критических точек распределения Фишера–Снедекора, по заданному уровню значимости 
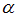и числам степеней свободы 
, 
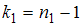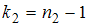найти критическую точку 
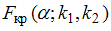. Если 
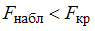– нет основания отвергнуть нулевую гипотезу. Если 
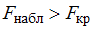– нулевую гипотезу отвергают.
Таким образом, при сравнении двух дисперсий нормальных генеральных совокупностей наблюдаемое значение критерия находится по таблице критических точек распределения Фишера–Снедекора.
Напомним правило, по которому проверяется гипотеза о равенстве генеральных дисперсий нормальных совокупностей.
Пусть по независимым выборкам, объемы которых
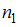и 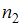, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперси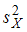и и 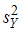. Требуется сравнить эти дисперсии.Напомним одно из правил, по которому проверяется гипотеза о равенстве генеральных дисперсий нормальных совокупностей:
Для того чтобы при заданном уровне значимости
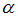проверить нулевую гипотезу 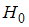: 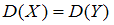о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе 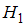: 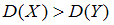, надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 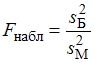и по таблице критических точек распределения Фишера–Снедекора, по заданному уровню значимости 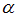и числам степеней свободы 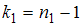, 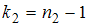найти критическую точку 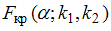. Если 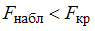– нет основания отвергнуть нулевую гипотезу. Если 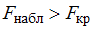– нулевую гипотезу отвергают.Таким образом, при сравнении двух дисперсий нормальных генеральных совокупностей наблюдаемое значение критерия находится по таблице критических точек распределения Фишера–Снедекора.
