Пусть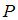 
– множество четных чисел, 
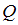– множество нечетных чисел. Тогда множеству 
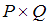принадлежит пара …
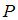– множество четных чисел, 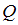– множество нечетных чисел. Тогда множеству 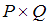принадлежит пара …
✓ 
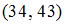
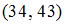
Решение:
Декартово произведение множеств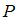
и 
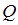– это множество всех упорядоченных пар, первая компонента которых принадлежит множеству 
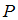, а вторая – множеству 
.
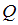В нашем случае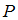
– множество четных чисел, 
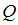– множество нечетных чисел. Значит, множество 
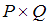будет состоять из пар, первая компонента которых является четным числом, а вторая компонента – нечетным числом. Среди перечисленных пар этому условию удовлетворяет только пара 
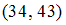, во всех остальных парах 
, 
, 
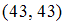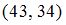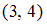первая компонента является нечетным числом.
Декартово произведение множеств
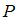и 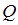– это множество всех упорядоченных пар, первая компонента которых принадлежит множеству 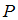, а вторая – множеству 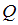.В нашем случае
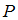– множество четных чисел, 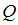– множество нечетных чисел. Значит, множество 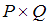будет состоять из пар, первая компонента которых является четным числом, а вторая компонента – нечетным числом. Среди перечисленных пар этому условию удовлетворяет только пара 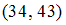, во всех остальных парах 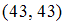, , 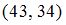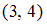первая компонента является нечетным числом.