Система линейных уравнений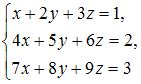 
…
…
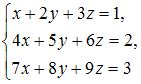✓ имеет бесконечное множество решений
Решение:
По методу Гаусса приведем расширенную матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:
Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг матрицы был равен рангу расширенной матрицы системы. В этом случае ранг матрицы системы равен двум и ранг расширенной матрицы системы также равен двум. Если ранг матрицы равен количеству неизвестных, то система является определенной, то есть имеет одно решение. Если же ранг совместной системы меньше числа неизвестных, т.е. 
то система неопределенная, то есть имеет больше одного решения. В нашем случае 
следовательно, система имеет бесконечное множество решений.
По методу Гаусса приведем расширенную матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:
Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг матрицы был равен рангу расширенной матрицы системы. В этом случае ранг матрицы системы равен двум и ранг расширенной матрицы системы также равен двум. Если ранг матрицы равен количеству неизвестных, то система является определенной, то есть имеет одно решение. Если же ранг совместной системы меньше числа неизвестных, т.е. то система неопределенная, то есть имеет больше одного решения. В нашем случае следовательно, система имеет бесконечное множество решений.