В урне 5 красных и 7 зеленых шаров. Из урны наудачу берут два шара. Вероятность того, что шары разноцветные, равна …
✓ 
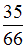
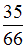
Решение:
Вероятностью события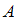
называется отношение числа элементарных исходов 
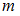, благоприятствующих данному событию, к числу 
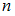равновозможных элементарных исходов испытания:
.
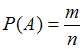В данной задаче событие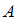
состоит в том, что из урны взяты два разноцветных шара, то есть 1 красный и 1 зеленый.
Вычислим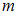
. Определим, сколькими способами можно взять 1 красный и 1 зеленый шар из имеющихся. Существует 5 способов извлечения красного шара и 7 способов извлечения зеленого шара. Для каждого извлеченного красного шара существует 7 способов извлечения зеленого шара. Поэтому общее число способов, которыми можно извлечь 2 шара разных цветов, равно 
.
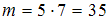Теперь найдем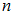
. Определим, сколькими способами можно взять два шара (
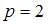) из имеющихся двенадцати шаров (
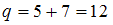). В этом нам поможет формула для нахождения числа сочетаний из 
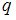элементов по 
: 
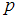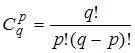. Получим 
.
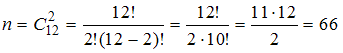Используя полученные значения, найдем вероятность события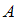
: 
.
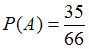Вероятностью события
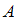называется отношение числа элементарных исходов 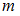, благоприятствующих данному событию, к числу 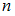равновозможных элементарных исходов испытания: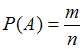.В данной задаче событие
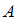состоит в том, что из урны взяты два разноцветных шара, то есть 1 красный и 1 зеленый.Вычислим
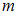. Определим, сколькими способами можно взять 1 красный и 1 зеленый шар из имеющихся. Существует 5 способов извлечения красного шара и 7 способов извлечения зеленого шара. Для каждого извлеченного красного шара существует 7 способов извлечения зеленого шара. Поэтому общее число способов, которыми можно извлечь 2 шара разных цветов, равно 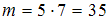.Теперь найдем
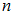. Определим, сколькими способами можно взять два шара (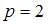) из имеющихся двенадцати шаров (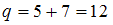). В этом нам поможет формула для нахождения числа сочетаний из 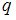элементов по 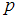: 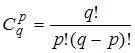. Получим 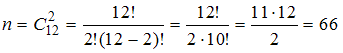. Используя полученные значения, найдем вероятность события
: .
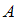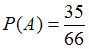