Даны числовые ряды:
А)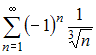
,
В)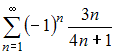
.
Тогда …
А)
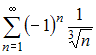,В)
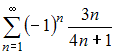.Тогда …
- ✓ ряд А) сходится, ряд В) расходится
Для исследования сходимости знакочередующегося ряда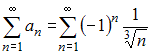 
применим признак сходимости Лейбница. Тогда:
1) вычислим предел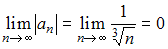
.
2) для любого натурального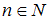
справедливо 
, то есть последовательность 
монотонно убывает.
Следовательно, ряд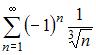
сходится.
Ряд
расходится, так как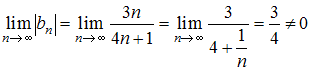 
.
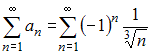применим признак сходимости Лейбница. Тогда:1) вычислим предел
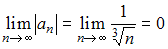.2) для любого натурального
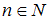справедливо , то есть последовательность монотонно убывает.Следовательно, ряд
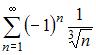сходится.Ряд
расходится, так как 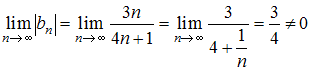.