Даны множества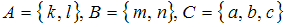 
. Тогда справедливо высказывание …
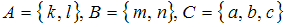. Тогда справедливо высказывание …
- ✓
Декартово произведение множеств 
– это множество 
всех упорядоченных троек элементов 
, первая компонента которых 
принадлежит множеству 
, вторая 
– множеству 
, а третья 
– множеству 
. Декартово произведение множеств не обладает свойством коммутативности, то есть, например, 
.
Определим истинность предложенных высказываний. Для этого установим, каким множествам принадлежат указанные тройки элементов.
Первый, второй и третий компоненты тройки
принадлежат множеству 
, значит, элемент 
принадлежит декартовому произведению множеств 
, и высказывание 
ложно.
Для тройки
имеем 
, 
,
. Следовательно, 
, и высказывание 
ложно.
Для тройки
имеем 
,
,
, значит, 
, и высказывание 
истинно.
Для тройки
имеем 
, 
, 
, значит, 
, и высказывание 
ложно.
Таким образом, справедливо только высказывание
.
– это множество всех упорядоченных троек элементов , первая компонента которых принадлежит множеству , вторая – множеству , а третья – множеству . Декартово произведение множеств не обладает свойством коммутативности, то есть, например, .Определим истинность предложенных высказываний. Для этого установим, каким множествам принадлежат указанные тройки элементов.
Первый, второй и третий компоненты тройки
принадлежат множеству , значит, элемент принадлежит декартовому произведению множеств , и высказывание ложно.Для тройки
имеем , ,. Следовательно, , и высказывание ложно.Для тройки
имеем ,,, значит, , и высказывание истинно.Для тройки
имеем , , , значит, , и высказывание ложно.Таким образом, справедливо только высказывание
.