Даны высказывания:
A = «Эйфелева башня находится в Париже»,
B = «Красноярск находится в Сибири»,
C = «Москва – столица России».
Из этих высказываний составлено новое высказывание «Если Эйфелева башня находится в Париже и Красноярск находится в Сибири, то Москва – столица России». Тогда, заменив в этом высказывании операцию импликации на операцию эквиваленции, получим высказывание:
A = «Эйфелева башня находится в Париже»,
B = «Красноярск находится в Сибири»,
C = «Москва – столица России».
Из этих высказываний составлено новое высказывание «Если Эйфелева башня находится в Париже и Красноярск находится в Сибири, то Москва – столица России». Тогда, заменив в этом высказывании операцию импликации на операцию эквиваленции, получим высказывание:
- ✓ «Эйфелева башня находится в Париже и Красноярск находится в Сибири тогда и только тогда, когда Москва – столица России»
Высказывание «Если Эйфелева башня находится в Париже и Красноярск находится в Сибири, то Москва – столица России» составлено из высказываний 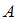 = «Эйфелева башня находится в Париже»,
= «Эйфелева башня находится в Париже», 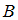 = «Красноярск находится в Сибири» и
= «Красноярск находится в Сибири» и 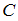 = «Москва – столица России» при помощи слов «если…, то…» и союза «и».
= «Москва – столица России» при помощи слов «если…, то…» и союза «и».
Высказывание, составленное из высказываний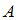 и
и 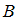 при помощи слов «если…, то…», называют импликацией высказываний и обозначают
при помощи слов «если…, то…», называют импликацией высказываний и обозначают 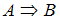 .
.
Высказывание, составленное из высказываний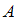 и
и 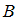 при помощи союза «и», называют конъюнкцией высказываний
при помощи союза «и», называют конъюнкцией высказываний 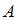 и
и 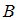 и обозначают
и обозначают 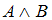 .
.
Высказывание, составленное из высказываний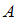 и
и 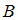 при помощи слов «…тогда и только тогда, когда…», называют эквиваленцией высказываний
при помощи слов «…тогда и только тогда, когда…», называют эквиваленцией высказываний 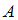 и
и 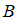 и обозначают
и обозначают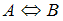 .
.
Наше высказывание имеет вид «Если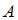 и
и 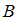 , то
, то 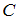 », значит, его формула с помощью символов логики высказываний запишется в виде
», значит, его формула с помощью символов логики высказываний запишется в виде 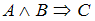 . Заменив операцию импликации на операцию эквиваленции, получим формулу
. Заменив операцию импликации на операцию эквиваленции, получим формулу 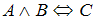 , которой соответствует высказывание «Эйфелева башня находится в Париже и Красноярск находится в Сибири тогда и только тогда, когда Москва – столица России».
, которой соответствует высказывание «Эйфелева башня находится в Париже и Красноярск находится в Сибири тогда и только тогда, когда Москва – столица России».
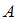 = «Эйфелева башня находится в Париже»,
= «Эйфелева башня находится в Париже», 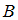 = «Красноярск находится в Сибири» и
= «Красноярск находится в Сибири» и 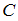 = «Москва – столица России» при помощи слов «если…, то…» и союза «и».
= «Москва – столица России» при помощи слов «если…, то…» и союза «и».Высказывание, составленное из высказываний
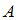 и
и 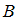 при помощи слов «если…, то…», называют импликацией высказываний и обозначают
при помощи слов «если…, то…», называют импликацией высказываний и обозначают 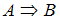 .
.Высказывание, составленное из высказываний
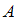 и
и 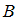 при помощи союза «и», называют конъюнкцией высказываний
при помощи союза «и», называют конъюнкцией высказываний 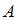 и
и 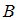 и обозначают
и обозначают 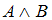 .
.Высказывание, составленное из высказываний
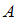 и
и 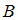 при помощи слов «…тогда и только тогда, когда…», называют эквиваленцией высказываний
при помощи слов «…тогда и только тогда, когда…», называют эквиваленцией высказываний 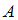 и
и 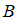 и обозначают
и обозначают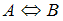 .
.Наше высказывание имеет вид «Если
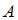 и
и 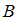 , то
, то 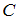 », значит, его формула с помощью символов логики высказываний запишется в виде
», значит, его формула с помощью символов логики высказываний запишется в виде 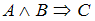 . Заменив операцию импликации на операцию эквиваленции, получим формулу
. Заменив операцию импликации на операцию эквиваленции, получим формулу 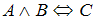 , которой соответствует высказывание «Эйфелева башня находится в Париже и Красноярск находится в Сибири тогда и только тогда, когда Москва – столица России».
, которой соответствует высказывание «Эйфелева башня находится в Париже и Красноярск находится в Сибири тогда и только тогда, когда Москва – столица России».