Дифференциальное уравнение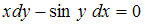 
в результате разделения переменных сводится к уравнению …
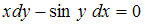в результате разделения переменных сводится к уравнению …
- ✓
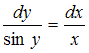
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде:
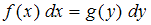. Такое уравнение решается путем интегрирования обеих частей уравнения.
Проведем разделение переменных в исходном уравнении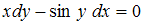
. Перенесем слагаемое, содержащее dx, в правую часть уравнения, получим уравнение 
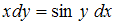. Разделим обе части уравнения на 
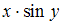. В результате получим уравнение с разделенными переменными 
.
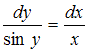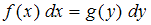. Такое уравнение решается путем интегрирования обеих частей уравнения.Проведем разделение переменных в исходном уравнении
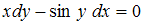. Перенесем слагаемое, содержащее dx, в правую часть уравнения, получим уравнение 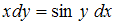. Разделим обе части уравнения на 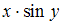. В результате получим уравнение с разделенными переменными .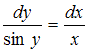