Для оценки с надежностью 
математического ожидания 
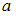нормально распределенного признака 
по выборочной средней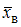 
при среднем квадратичном отклонении 
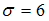генеральной совокупности используют доверительный интервал 
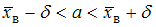, где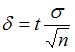 
– точность оценки, 
– объем выборки, 
– значение аргумента функции Лапласа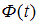 
, при котором 
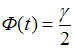. Значение аргумента функции Лапласа для 
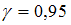равно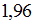 
.
Установите соответствие между доверительными интервалами и объемом выборки
.
1.
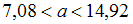
2.
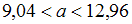
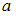математического ожидания нормально распределенного признака по выборочной средней 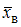при среднем квадратичном отклонении 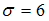генеральной совокупности используют доверительный интервал 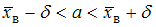, где 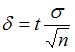– точность оценки, – объем выборки, – значение аргумента функции Лапласа 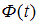, при котором 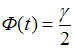. Значение аргумента функции Лапласа для 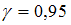равно 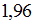.Установите соответствие между доверительными интервалами и объемом выборки
.1.
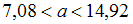
2.
- ✓
- ✓
- ✓
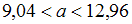
Используем формулу доверительного интервала 
для нахождения точности 
.
Очевидно, что разность между правой и левой границами дает удвоенную точность, то есть
.
Для доверительного интервала
имеем 
. Следовательно, 
. Из условия задачи имеем 
, а при 
и 
получим 
. Откуда 
.
Для доверительного интервала
имеем 
. Следовательно, 
. Из формулы 
получим 
. Откуда 
.
Следовательно, доверительному интервалу
соответствует выборка объемом 4, а интервал 
вычислен для выборки объемом 16.
для нахождения точности . Очевидно, что разность между правой и левой границами дает удвоенную точность, то есть
.Для доверительного интервала
имеем . Следовательно, . Из условия задачи имеем , а при и получим . Откуда .Для доверительного интервала
имеем . Следовательно, . Из формулы получим . Откуда .Следовательно, доверительному интервалу
соответствует выборка объемом 4, а интервал вычислен для выборки объемом 16.