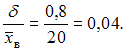Для оценки с некоторой надежностью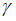 
математического ожидания a нормально распределенного признака X по выборочной средней 
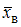использовали доверительный интервал 
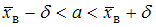, где 
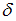– точность оценки.
Установите соответствие между доверительными интервалами и значениями относительной точности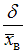
:
1)
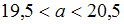
2)
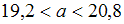
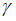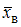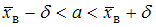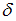математического ожидания a нормально распределенного признака X по выборочной средней использовали доверительный интервал , где – точность оценки.Установите соответствие между доверительными интервалами и значениями относительной точности
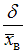:1)
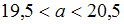
2)
- ✓
- ✓
- ✓
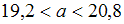
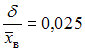
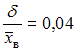
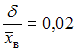
Рассмотрим доверительный интервал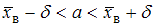 
.
Заметим, что при сложении левой и правой частей интервала имеем:
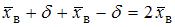; при вычитании из значения правой границы интервала значения его левой границы получим 
.
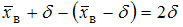Для интервала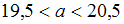
определим 
, 
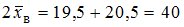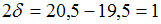. Отсюда 
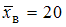и 
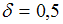. Соответствующее значение относительной точности равно 
.
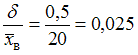Для интервала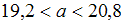
определим 
, 
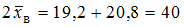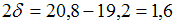. Отсюда 
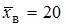и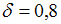 
. Соответствующее значение относительной точности равно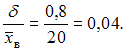 
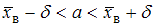.Заметим, что при сложении левой и правой частей интервала имеем:
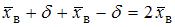; при вычитании из значения правой границы интервала значения его левой границы получим 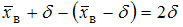.Для интервала
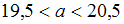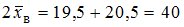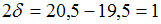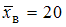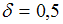определим , . Отсюда и . Соответствующее значение относительной точности равно 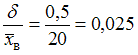.Для интервала
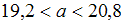определим 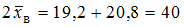, 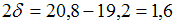. Отсюда 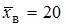и 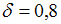. Соответствующее значение относительной точности равно 