Два автомата производят одинаковые детали, поступающие на общий конвейер. Детали, произведенные на первом станке (событие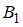 
), составляют 
деталей, произведенных обоими станками. Причем первый станок производит в среднем 60% стандартных деталей, а второй – 80%. Наудачу выбранная деталь оказалась стандартной (событие 
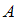). Для определения вероятности того, что стандартная деталь была изготовлена на первом станке, использована формула Бейеса 
.
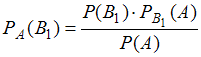Установите соответствие между обозначениями вероятностей и их значениями.
1.
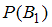
2.
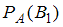
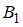), составляют деталей, произведенных обоими станками. Причем первый станок производит в среднем 60% стандартных деталей, а второй – 80%. Наудачу выбранная деталь оказалась стандартной (событие 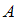). Для определения вероятности того, что стандартная деталь была изготовлена на первом станке, использована формула Бейеса 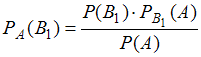.Установите соответствие между обозначениями вероятностей и их значениями.
1.
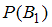
2.
- ✓
- ✓
- ✓
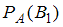
Для решения задачи используется формула Бейеса. Пусть событие 
может наступить лишь при условии появления одного из 
несовместных событий (гипотез) 
, 
, …, 
, образующих полную группу. Если событие 
уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
,
где
. В формуле использованы обозначения 
– вероятность события 
; 
– условная вероятность события 
, то есть вероятность события 
, вычисленная в предположении, что событие 
наступило.
Событие
в данной задаче состоит в том, что деталь признана стандартной. Гипотеза 
: деталь изготовлена на первом станке.
Гипотеза
: деталь изготовлена на втором станке.
Так как на первом станке изготавливается
всех произведенных деталей, то 
.
Тогда
.
Причем условная вероятность того, что деталь, изготовленная на первом станке, оказалась стандартной, составляет 60%. Напомним, что
, поэтому 
.
Условная вероятность того, что деталь, изготовленная на втором станке, оказалась стандартной, составляет 80%, то есть
.
Подставив данные в формулу Бейеса, имеем
.
может наступить лишь при условии появления одного из несовместных событий (гипотез) , , …, , образующих полную группу. Если событие уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса,где
. В формуле использованы обозначения – вероятность события ; – условная вероятность события , то есть вероятность события , вычисленная в предположении, что событие наступило.Событие
в данной задаче состоит в том, что деталь признана стандартной. Гипотеза : деталь изготовлена на первом станке.Гипотеза
: деталь изготовлена на втором станке.Так как на первом станке изготавливается
всех произведенных деталей, то .Тогда
.Причем условная вероятность того, что деталь, изготовленная на первом станке, оказалась стандартной, составляет 60%. Напомним, что
, поэтому .Условная вероятность того, что деталь, изготовленная на втором станке, оказалась стандартной, составляет 80%, то есть
.Подставив данные в формулу Бейеса, имеем
.