Иванов и Петров производят заполнение контейнеров энергосберегающими лампами с «холодным» свечением. Иванов успевает заполнить 7 контейнеров из 15, в то время как Петров заполняет 8 остальных контейнеров. Вероятность того, что Иванов упакует лампу с «теплым» свечением, равна 0,03, а Петров –  . В выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.
. В выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.
Установите соответствие между значениями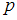 и вероятностью того, что контейнер заполнял лампами Иванов:
и вероятностью того, что контейнер заполнял лампами Иванов:
1)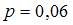 ,
,
2) .
.
 . В выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.
. В выбранном наудачу контейнере обнаружили лампу с «теплым» свечением. Установите соответствие между значениями
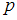 и вероятностью того, что контейнер заполнял лампами Иванов:
и вероятностью того, что контейнер заполнял лампами Иванов:1)
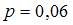 ,
,2)
 .
.
- ✓
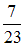
- ✓
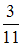
- ✓
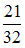
Для решения задачи необходимо воспользоваться формулой Бейеса. Пусть событие 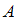 может наступить лишь при условии появления одного из
может наступить лишь при условии появления одного из 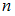 несовместных событий (гипотез)
несовместных событий (гипотез) 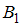 ,
, 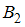 , …,
, …, 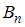 , образующих полную группу. Если событие
, образующих полную группу. Если событие 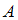 уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
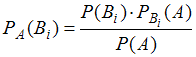 ,
,
где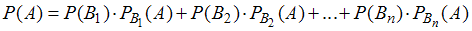 . В формуле использованы обозначения
. В формуле использованы обозначения 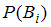 – вероятность события
– вероятность события 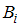 ;
; 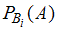 – условная вероятность события
– условная вероятность события 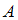 , то есть вероятность события
, то есть вероятность события 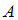 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 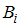 наступило.
наступило.
Событие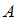 в данной задаче состоит в том, что в выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.
в данной задаче состоит в том, что в выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.
Гипотеза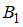 : контейнер заполнял Иванов.
: контейнер заполнял Иванов.
Гипотеза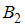 : контейнер заполнял Петров.
: контейнер заполнял Петров.
Искомые вероятности найдем по формуле Бейеса:
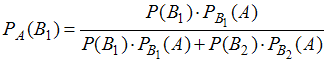 .
.
Из условия задачи имеем:
вероятность заполнения контейнера Ивановым равна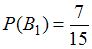 ;
;
вероятность заполнения контейнера Петровым равна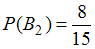 .
.
Условная вероятность того, что Иванов упакует лампу с «теплым» свечением, равна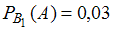 .
.
Условная вероятность того, что Петров упакует лампу с «теплым» свечением, равна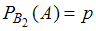 .
.
Подставив данные в формулу Бейеса, получим
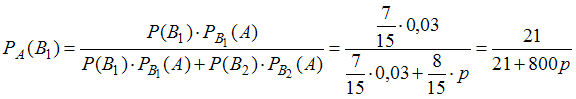 .
.
Вычислим для конкретного значения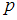 .
.
Если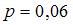 , то
, то 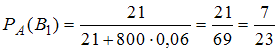 .
.
Если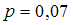 , то
, то 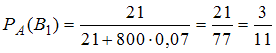 .
.
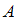 может наступить лишь при условии появления одного из
может наступить лишь при условии появления одного из 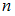 несовместных событий (гипотез)
несовместных событий (гипотез) 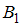 ,
, 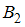 , …,
, …, 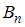 , образующих полную группу. Если событие
, образующих полную группу. Если событие 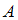 уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса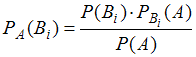 ,
,где
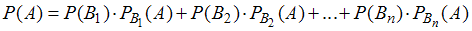 . В формуле использованы обозначения
. В формуле использованы обозначения 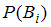 – вероятность события
– вероятность события 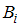 ;
; 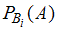 – условная вероятность события
– условная вероятность события 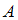 , то есть вероятность события
, то есть вероятность события 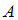 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 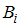 наступило.
наступило.Событие
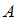 в данной задаче состоит в том, что в выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.
в данной задаче состоит в том, что в выбранном наудачу контейнере обнаружили лампу с «теплым» свечением.Гипотеза
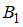 : контейнер заполнял Иванов.
: контейнер заполнял Иванов.Гипотеза
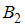 : контейнер заполнял Петров.
: контейнер заполнял Петров.Искомые вероятности найдем по формуле Бейеса:
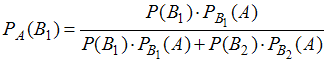 .
.Из условия задачи имеем:
вероятность заполнения контейнера Ивановым равна
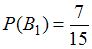 ;
;вероятность заполнения контейнера Петровым равна
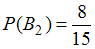 .
.Условная вероятность того, что Иванов упакует лампу с «теплым» свечением, равна
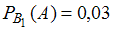 .
.Условная вероятность того, что Петров упакует лампу с «теплым» свечением, равна
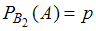 .
.Подставив данные в формулу Бейеса, получим
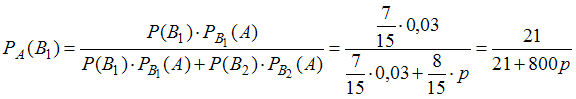 .
.Вычислим для конкретного значения
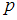 .
.Если
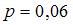 , то
, то 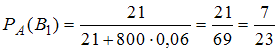 .
.Если
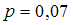 , то
, то 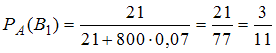 .
.