Математика и статистика
Тестовый вопрос
На множестве заданы отношения P = « x и y оканчиваются одной и той же цифрой», R = « x больше y » и Q = « x не делится на y ». Тогда двум из этих отношений принадлежат пары
Варианты ответа
Ответ проверенНа множестве 
заданы отношения P = « x и y оканчиваются одной и той же цифрой», R = « x больше y » и Q = « x не делится на y ». Тогда двум из этих отношений принадлежат пары …
заданы отношения P = « x и y оканчиваются одной и той же цифрой», R = « x больше y » и Q = « x не делится на y ». Тогда двум из этих отношений принадлежат пары …
- (12, 22)
- (21, 12)
Бинарным отношением, заданным на множестве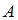 
, называется всякое подмножество декартова произведения 
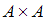. Некоторая упорядоченная пара будет принадлежать данному отношению, если при подстановке первого элемента пары вместо 
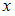, а второго элемента вместо 
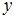получится истинное высказывание.
Определим, каким отношениям принадлежит каждая из предложенных пар.
Для этого подставим элементы каждой из пар в предложенные отношения и определим значение истинности полученных высказываний.
При подстановке пары (21, 22) в отношения P = «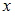
и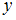 
оканчиваются одной и той же цифрой», R = «
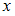больше 
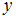», Q = «
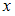не делится на 
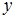» получим высказывания «21 и 22 оканчиваются одной и той же цифрой», «21 больше 22», «21 не делится на 22». Первые два высказывания ложны, а третье истинно, то есть пара (21, 22) принадлежит только одному из данных отношений.
При подстановке пары (21, 12) получим высказывания «21 и 12 оканчиваются одной и той же цифрой», «21 больше 12», «21 не делится на 12». Первое высказывание ложно, а второе и третье истинны, то есть пара (21, 22) принадлежит двум из данных отношений.
При подстановке пары (12, 22) получим высказывания «12 и 22 оканчиваются одной и той же цифрой», «12 больше 22», «12 не делится на 22». Первое и третье высказывания истинны, а второе ложно, то есть пара (12, 22) принадлежит двум из данных отношений.
При подстановке пары (22, 12) получим высказывания «22 и 12 оканчиваются одной и той же цифрой», «22 больше 12», «22 не делится на 12». Все три высказывания истинны, то есть пара (22, 12) принадлежит всем трем отношениям.
Таким образом, двум из данных отношений принадлежат пары (12, 22) и (21, 12).
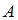, называется всякое подмножество декартова произведения 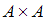. Некоторая упорядоченная пара будет принадлежать данному отношению, если при подстановке первого элемента пары вместо 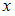, а второго элемента вместо 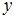получится истинное высказывание.Определим, каким отношениям принадлежит каждая из предложенных пар.
Для этого подставим элементы каждой из пар в предложенные отношения и определим значение истинности полученных высказываний.
При подстановке пары (21, 22) в отношения P = «
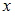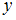и оканчиваются одной и той же цифрой», R = « 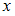больше 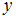», Q = « 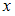не делится на 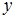» получим высказывания «21 и 22 оканчиваются одной и той же цифрой», «21 больше 22», «21 не делится на 22». Первые два высказывания ложны, а третье истинно, то есть пара (21, 22) принадлежит только одному из данных отношений.При подстановке пары (21, 12) получим высказывания «21 и 12 оканчиваются одной и той же цифрой», «21 больше 12», «21 не делится на 12». Первое высказывание ложно, а второе и третье истинны, то есть пара (21, 22) принадлежит двум из данных отношений.
При подстановке пары (12, 22) получим высказывания «12 и 22 оканчиваются одной и той же цифрой», «12 больше 22», «12 не делится на 22». Первое и третье высказывания истинны, а второе ложно, то есть пара (12, 22) принадлежит двум из данных отношений.
При подстановке пары (22, 12) получим высказывания «22 и 12 оканчиваются одной и той же цифрой», «22 больше 12», «22 не делится на 12». Все три высказывания истинны, то есть пара (22, 12) принадлежит всем трем отношениям.
Таким образом, двум из данных отношений принадлежат пары (12, 22) и (21, 12).
Похожие вопросы из темы
Вся тема «Математика и статистика» →
Дано логическое выражение . Тогда функциональная схема, соответствующая этому логическому выражению, может иметь вид
Свойство оценок, при котором среднее выборочного распределения оценки равно величине оцениваемого параметра, называется:
равен:
Система линейных уравнений имеет единственное решение, если не равно
Пересечение множеств, задаваемых уравнениями 2х + у = 3 и у — 3х = 3, есть:
За пределы значений частных индексов не может выходить индекс …