На множестве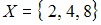 
заданы отношения 
= «
», 
= «
», 
= «
», 
= «
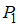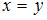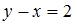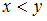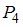». Тогда наименьшее число пар принадлежит отношениям …
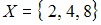заданы отношения 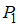= «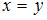», = «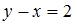», 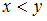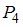= «», = «». Тогда наименьшее число пар принадлежит отношениям …
- ✓
- ✓
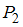
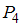
Бинарным отношением, заданным на множестве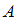 
, называется всякое подмножество декартова произведения 
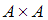. Некоторая упорядоченная пара будет принадлежать данному отношению, если при подстановке первого элемента пары вместо 
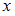, а второго элемента вместо 
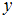получится истинное высказывание.
Определим, какие пары будут принадлежать каждому из отношений.
Рассмотрим отношение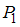
= «
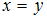». Найдем пары, первая и вторая компонента которых равны, а сами компоненты принадлежат множеству 
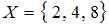. Получим пары: 
, 
, 
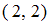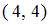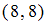. При подстановке элементов этих пар в данное отношение получатся истинные высказывания «
», «
», «
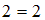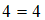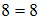». Следовательно, отношение 
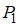содержит 3 пары.
Рассмотрим отношение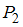
= «
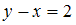». Найдем пары, у которых разность второй и первой компонент равна 2, а сами компоненты принадлежат множеству 
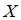. Получим единственную пару 
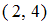. При подстановке элементов этой пары в данное отношение получится истинное высказывание «
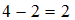». Следовательно, отношение 
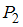содержит 1 пару.
Рассмотрим отношение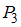
= «
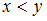». Найдем пары, первая компонента которых меньше второй, а сами компоненты принадлежат множеству 
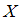. Получим пары: 
, 
, 
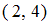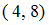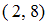. При подстановке элементов этих пар в данное отношение получатся истинные высказывания: «
», «
», «
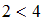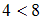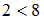». Следовательно, отношение 
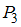содержит 3 пары.
Рассмотрим отношение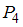
= «
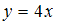». Найдем пары, вторая компонента которых больше первой в 4 раза, а сами компоненты принадлежат множеству 
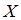. Получим единственную пару 
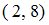. При подстановке элементов этой пары в данное отношение получится истинное высказывание «
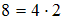». Следовательно, отношение 
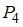содержит 1 пару.
Таким образом, наименьшее число пар (одна) принадлежит отношениям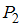
и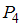 
.
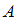, называется всякое подмножество декартова произведения 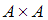. Некоторая упорядоченная пара будет принадлежать данному отношению, если при подстановке первого элемента пары вместо 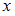, а второго элемента вместо 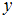получится истинное высказывание.Определим, какие пары будут принадлежать каждому из отношений.
Рассмотрим отношение
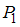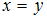= «». Найдем пары, первая и вторая компонента которых равны, а сами компоненты принадлежат множеству 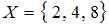. Получим пары: 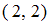, , 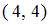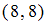. При подстановке элементов этих пар в данное отношение получатся истинные высказывания «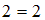», «», «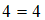»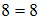. Следовательно, отношение 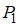содержит 3 пары.Рассмотрим отношение
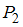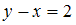= «». Найдем пары, у которых разность второй и первой компонент равна 2, а сами компоненты принадлежат множеству 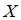. Получим единственную пару 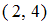. При подстановке элементов этой пары в данное отношение получится истинное высказывание «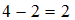». Следовательно, отношение 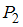содержит 1 пару.Рассмотрим отношение
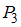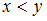= «». Найдем пары, первая компонента которых меньше второй, а сами компоненты принадлежат множеству 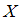. Получим пары: 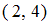, , 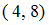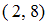. При подстановке элементов этих пар в данное отношение получатся истинные высказывания: «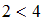», «», «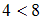»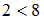. Следовательно, отношение 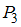содержит 3 пары.Рассмотрим отношение
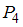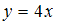= «». Найдем пары, вторая компонента которых больше первой в 4 раза, а сами компоненты принадлежат множеству 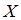. Получим единственную пару 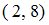. При подстановке элементов этой пары в данное отношение получится истинное высказывание «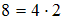». Следовательно, отношение 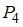содержит 1 пару.Таким образом, наименьшее число пар (одна) принадлежит отношениям
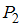и 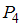.