Неявная функция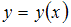 
определяется как решение уравнения 
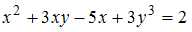. Тогда производная первого порядка 
при 
равна …
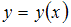определяется как решение уравнения 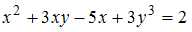. Тогда производная первого порядка при равна …
- ✓ 0
Продифференцируем по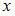 
обе части уравнения 
.
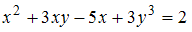Тогда
.
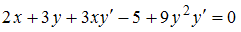Решим последнее уравнение относительно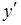
, получаем
.
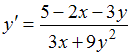Подставив значение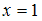
в уравнение 
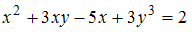, получаем 
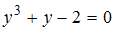, то есть 
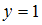. Тогда 
.
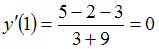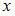обе части уравнения 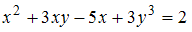. Тогда
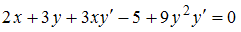. Решим последнее уравнение относительно
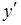, получаем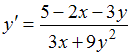.Подставив значение
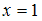в уравнение 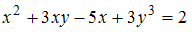, получаем 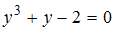, то есть 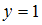. Тогда .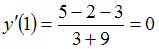