Обе пары (6, 2) и (2, 6) принадлежат отношениям …
- ✓ «
» - ✓ «
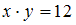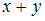делится на 4»
Некоторая упорядоченная пара будет принадлежать данному отношению, если при подстановке первого элемента пары вместо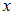 
, а второго элемента вместо 
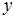получится истинное высказывание.
Подставим элементы каждой из пар (6, 2), (2, 6) в предложенные отношения и определим значения истинности полученных высказываний.
При подстановке в отношение «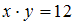
» получим высказывания «
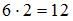» и «
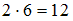», которые истинны, то есть обе пары принадлежат этому отношению.
При подстановке в отношение «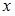
меньше 
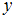» получим высказывания «6 меньше 2» и «2 меньше 6», первое из которых ложно, а второе истинно, то есть данному отношению принадлежит только одна пара.
При подстановке в отношение «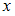
и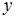 
меньше 5» получим высказывания «6 и 2 меньше 5» и «2 и 6 меньше 5», которые ложны, то есть данные пары не принадлежат этому отношению.
При подстановке в отношение «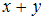
делится на 4» получим высказывания «6+2 делится на 4» и «2+6 делится на 4», которые истинны, то есть обе пары принадлежат этому отношению.
Таким образом, обе пары (6, 2) и (2, 6) принадлежат отношениям «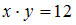
» и «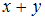
делится на 4».
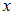, а второго элемента вместо 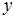получится истинное высказывание.Подставим элементы каждой из пар (6, 2), (2, 6) в предложенные отношения и определим значения истинности полученных высказываний.
При подстановке в отношение «
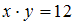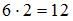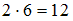» получим высказывания «» и «», которые истинны, то есть обе пары принадлежат этому отношению.При подстановке в отношение «
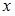меньше 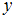» получим высказывания «6 меньше 2» и «2 меньше 6», первое из которых ложно, а второе истинно, то есть данному отношению принадлежит только одна пара.При подстановке в отношение «
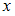и 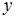меньше 5» получим высказывания «6 и 2 меньше 5» и «2 и 6 меньше 5», которые ложны, то есть данные пары не принадлежат этому отношению.При подстановке в отношение «
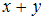делится на 4» получим высказывания «6+2 делится на 4» и «2+6 делится на 4», которые истинны, то есть обе пары принадлежат этому отношению.Таким образом, обе пары (6, 2) и (2, 6) принадлежат отношениям «
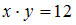» и «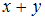 делится на 4».