Отрицательно определенная квадратичная форма может иметь вид …
- ✓
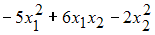
Квадратичная форма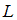 
называется отрицательно определенной, если при всех значениях переменных 
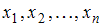, из которых хотя бы одно отлично от нуля, 
.
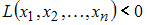1) Для квадратичной формы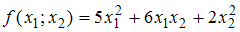
характеристическое уравнение 
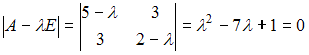имеет положительные корни 
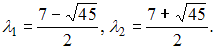Следовательно, квадратичная форма 
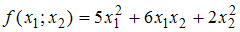является знакоположительной.
2) Для квадратичной формы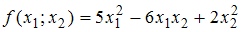
характеристическое уравнение 
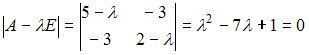имеет положительные корни 
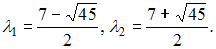Следовательно, квадратичная форма 
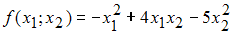является знакоположительной.
3) Для квадратичной формы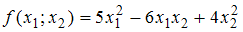
характеристическое уравнение 
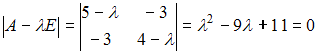имеет положительные корни 
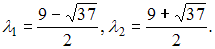Следовательно, квадратичная форма 
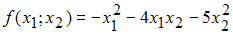является знакоположительной.
4) Для квадратичной формы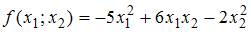
характеристическое уравнение 
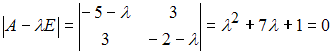имеет отрицательные корни 
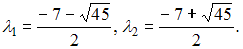Следовательно, 
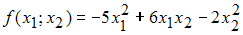является отрицательно определенной квадратичной формой.
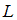называется отрицательно определенной, если при всех значениях переменных 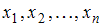, из которых хотя бы одно отлично от нуля, 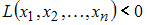.1) Для квадратичной формы
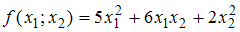характеристическое уравнение 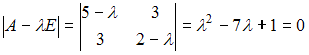имеет положительные корни 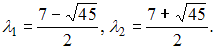Следовательно, квадратичная форма 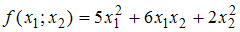является знакоположительной.2) Для квадратичной формы
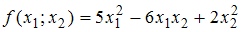характеристическое уравнение 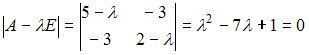имеет положительные корни 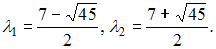Следовательно, квадратичная форма 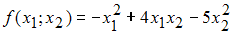является знакоположительной.3) Для квадратичной формы
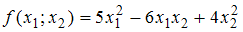характеристическое уравнение 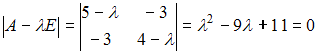имеет положительные корни 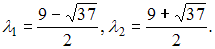Следовательно, квадратичная форма 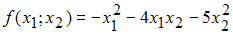является знакоположительной.4) Для квадратичной формы
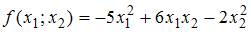характеристическое уравнение 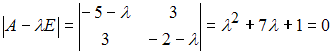имеет отрицательные корни 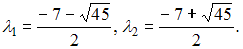Следовательно, 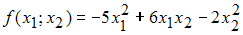является отрицательно определенной квадратичной формой.