Площадь треугольника, образованного пересечением прямой 
с осями координат, равна …
с осями координат, равна …
- ✓ 54
Приведем уравнение прямой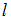 
к уравнению прямой «в отрезках»: 
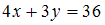или 
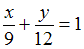. Уравнение прямой «в отрезках», отсекающей на координатных осях 
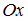и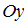 
отрезки длино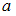й 
и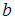 
соответственно, имеет вид: 
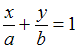. Следовательно, треугольник, образованный прямой 
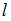и осями координат – прямоугольный, с вершинами 
, 
, 
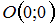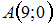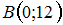и гипотенузой 
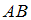. Площадь треугольника 
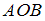будет равна: 
.
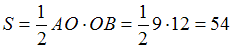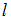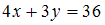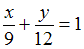к уравнению прямой «в отрезках»: или . Уравнение прямой «в отрезках», отсекающей на координатных осях 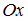и 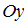отрезки длино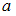й и 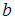соответственно, имеет вид: 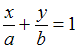. Следовательно, треугольник, образованный прямой 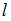и осями координат – прямоугольный, с вершинами 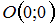, , 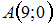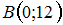и гипотенузой 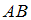. Площадь треугольника 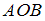будет равна: .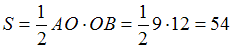