Математика и статистика
Тестовый вопрос
Упорядоченные пары (6, 3), (8, 4), (12, 4) принадлежат отношениям
Варианты ответа
Ответ из базыУпорядоченные пары (6, 3), (8, 4), (12, 4) принадлежат отношениям …
- «
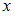делится на 
» - «
»
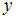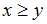Некоторая упорядоченная пара будет принадлежать данному отношению, если при подстановке первого элемента пары вместо 
, а второго элемента вместо 
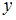получится истинное высказывание.
Подставим элементы данных пар (6, 3), (8, 4), (12, 4) в отношение «
делится на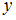 
». Получим высказывания «6 делится на 3», «8 делится на 4», «12 делится на 4», каждое из которых истинно.
Для отношения «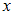
– делитель 
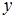» получим высказывания «6 – делитель 3», «8 – делитель 4» и «12 – делитель 4», которые ложны.
Для отношения «
» получим высказывания «
», «
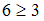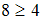» и «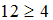
», каждое из которых истинно.
Для отношения «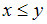
» получим высказывания «
», «
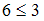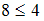» и «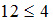
», которые ложны.
Таким образом, каждая из пар (6, 3), (8, 4), (12, 4) принадлежит отношениям «
делится на 
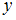» и «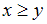
».
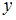, а второго элемента вместо получится истинное высказывание.Подставим элементы данных пар (6, 3), (8, 4), (12, 4) в отношение «
делится на 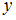». Получим высказывания «6 делится на 3», «8 делится на 4», «12 делится на 4», каждое из которых истинно.Для отношения «
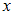– делитель 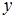» получим высказывания «6 – делитель 3», «8 – делитель 4» и «12 – делитель 4», которые ложны.Для отношения «
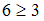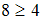» получим высказывания «», «» и «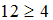», каждое из которых истинно.Для отношения «
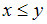» получим высказывания «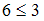», «» 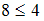и «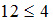», которые ложны.Таким образом, каждая из пар (6, 3), (8, 4), (12, 4) принадлежит отношениям «
делится на 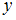» и «».Дата изменения страницы не означает экспертную проверку ответа. Как проверять материалы.
Сообщить об ошибке или предложить уточнение
К вопросу № 72 352. Адрес этой страницы будет добавлен автоматически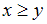.