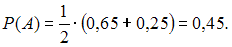В двух одинаковых коробках упакованы баночки с йогуртом. Вероятность того, что в первой коробке окажутся баночки с истекшим сроком хранения, равна p, а вероятность наличия такой продукции для второй коробки равна 0,25. Установите соответствие между значениями p и вероятностью того, что выбранная случайным образом баночка из наугад выбранной коробки оказалась с истекшим сроком хранения:
1) p = 0,15
2) p = 0,65
1) p = 0,15
2) p = 0,65
- ✓ 0,2
- ✓ 0,45
- ✓ 0,5
Рассмотрим событие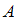 
– выбранная случайным образом баночка оказалась с истекшим сроком хранения. Оно может произойти, если баночка была извлечена из первой коробки (событие 
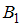) или из второй коробки (событие 
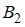). Заметим, что события 
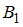и 
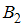несовместны, поскольку баночка извлекается только один раз.
В этом случае вероятность события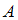
может быть определена при помощи формулы полной вероятности: 
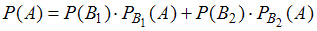, где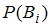 
– вероятность события 
; 
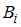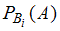– условная вероятность события 
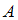, то есть вероятность события 
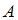, вычисленная в предположении, что событие 
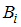наступило.
События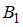
и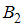 
равновозможны, поскольку коробка выбирается наугад. Таким образом,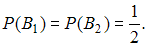 
Согласно условию, вероятность того, что в первой коробке окажутся баночки с истекшим сроком хранения, равна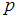
, поэтому вероятность извлечь баночку с просроченным йогуртом из первой коробки равна 
.
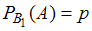Аналогично вероятность извлечения баночки с истекшим сроком хранения из второй коробки равна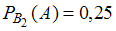
.
При подстановке в формулу полной вероятности получим: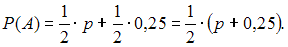
Рассчитаем вероятность события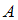
:
при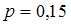
:
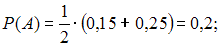
при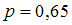
:
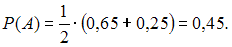
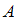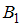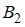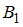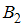– выбранная случайным образом баночка оказалась с истекшим сроком хранения. Оно может произойти, если баночка была извлечена из первой коробки (событие ) или из второй коробки (событие ). Заметим, что события и несовместны, поскольку баночка извлекается только один раз.В этом случае вероятность события
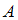может быть определена при помощи формулы полной вероятности: 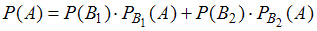, где 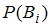– вероятность события 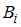; 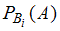– условная вероятность события 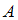, то есть вероятность события 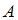, вычисленная в предположении, что событие 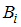наступило.События
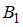и 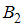равновозможны, поскольку коробка выбирается наугад. Таким образом,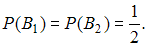 Согласно условию, вероятность того, что в первой коробке окажутся баночки с истекшим сроком хранения, равна
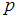, поэтому вероятность извлечь баночку с просроченным йогуртом из первой коробки равна 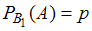.Аналогично вероятность извлечения баночки с истекшим сроком хранения из второй коробки равна
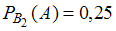.При подстановке в формулу полной вероятности получим:
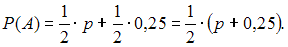
Рассчитаем вероятность события
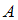:при
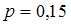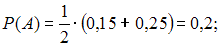
:при
:
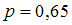