Варианты с частотой 3 содержат выборки …
- ✓ 1, 1, 2, 2, 3, 3, 4, 4, 4, 6
- ✓ 5, 5, 5, 6, 7, 7, 8
Вариантами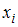 
называются наблюдаемые значения рассматриваемого признака. Частота варианты 
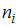указывает, сколько раз варианта повторяется в выборке. Для удобства составим статистические распределения для каждой выборки.
Статистическим распределением выборки называют перечень вариант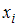
и соответствующих им частот 
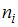, который записывается в виде таблицы: 
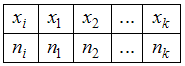. Индекс 
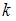указывает количество различных вариант, встречающихся в выборке.
Для выборки 1, 1, 2, 2, 3, 3, 4, 4, 4, 6 имеем следующие значения вариант и их частот:
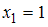(встречается дважды, то есть 
);
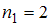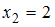(встречается дважды, то есть 
);
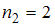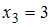(встречается дважды, то есть 
);
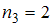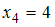(встречается трижды, то есть 
);
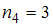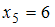(встречается один раз, то есть 
).
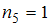Статистическое распределение имеет вид:
.
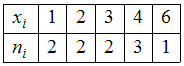Заметим, что варианта 4 имеет частоту 3.
Для выборки 5, 5, 5, 6, 7, 7, 8 имеем следующие значения вариант и их частот:
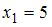(встречается трижды, то есть 
);
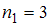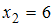(встречается один раз, то есть 
);
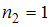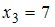(встречается дважды, то есть 
);
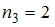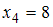(встречается один раз, то есть 
).
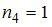Статистическое распределение имеет вид:
.
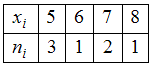Заметим, что варианта 5 имеет частоту 3.
Для выборки 1, 2, 2, 3, 3, 3, 3, 4, 6 имеем следующие значения вариант и их частот:
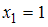(встречается один раз, то есть 
),
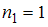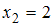(встречается дважды, то есть 
),
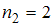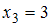(встречается четыре раза, то есть 
),
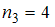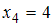(встречается один раз, то есть 
),
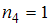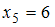(встречается один раз, то есть 
).
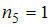Статистическое распределение имеет вид:
.
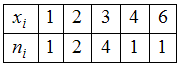Нет вариант, имеющих частоту 3.
Для выборки 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7 имеем следующие значения вариант и их частот:
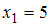(встречается пять раз, то есть 
),
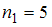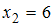(встречается четыре раза, то есть 
),
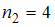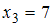(встречается дважды, то есть 
).
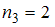Статистическое распределение имеет вид:
.
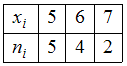Нет вариант, имеющих частоту 3.
Таким образом, варианты с частотой 3 содержат следующие выборки: 1, 1, 2, 2, 3, 3, 4, 4, 4, 6 и 5, 5, 5, 6, 7, 7, 8.
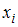называются наблюдаемые значения рассматриваемого признака. Частота варианты 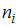указывает, сколько раз варианта повторяется в выборке. Для удобства составим статистические распределения для каждой выборки.Статистическим распределением выборки называют перечень вариант
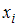и соответствующих им частот 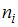, который записывается в виде таблицы: 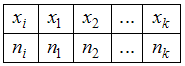. Индекс 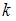указывает количество различных вариант, встречающихся в выборке.Для выборки 1, 1, 2, 2, 3, 3, 4, 4, 4, 6 имеем следующие значения вариант и их частот:
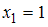(встречается дважды, то есть 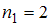); 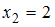(встречается дважды, то есть 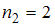); 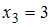(встречается дважды, то есть 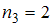); 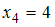(встречается трижды, то есть 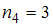); 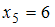(встречается один раз, то есть 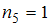).Статистическое распределение имеет вид:
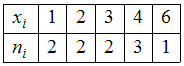.Заметим, что варианта 4 имеет частоту 3.
Для выборки 5, 5, 5, 6, 7, 7, 8 имеем следующие значения вариант и их частот:
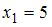(встречается трижды, то есть 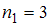); 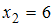(встречается один раз, то есть 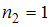); 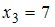(встречается дважды, то есть 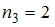); 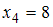(встречается один раз, то есть 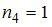).Статистическое распределение имеет вид:
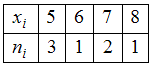.Заметим, что варианта 5 имеет частоту 3.
Для выборки 1, 2, 2, 3, 3, 3, 3, 4, 6 имеем следующие значения вариант и их частот:
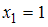(встречается один раз, то есть 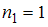), 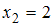(встречается дважды, то есть 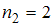), 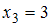(встречается четыре раза, то есть 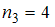), 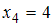(встречается один раз, то есть 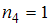), 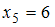(встречается один раз, то есть 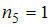).Статистическое распределение имеет вид:
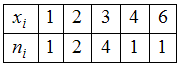.Нет вариант, имеющих частоту 3.
Для выборки 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7 имеем следующие значения вариант и их частот:
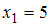(встречается пять раз, то есть 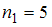), 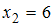(встречается четыре раза, то есть 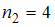), 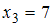(встречается дважды, то есть 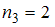).Статистическое распределение имеет вид:
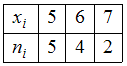.Нет вариант, имеющих частоту 3.
Таким образом, варианты с частотой 3 содержат следующие выборки: 1, 1, 2, 2, 3, 3, 4, 4, 4, 6 и 5, 5, 5, 6, 7, 7, 8.
