Выборочная средняя выборки, полигон относительных частот которой задан на рисунке
,
равна …
,равна …
- ✓ 3,3
Выборочной средней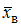 
называют среднее арифметическое значение признака выборочной совокупности, которое вычисляют по формуле 
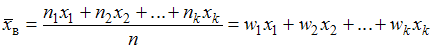, где 
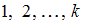– номера вариант, 
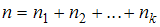– объем выборки. Наблюдаемые значения рассматриваемого признака 
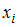называются вариантами. Количество наблюдений данной варианты – частота 
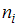. Отношения числа наблюдений к объему выборки 
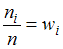называют относительными частотами.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки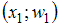
, 
, …, 
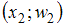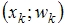. По полигону относительных частот находим координаты точек: 
; 
, 
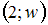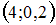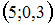. Значение неизвестной относительной частоты найдем, используя соотношение:
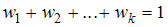, то есть 
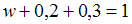, отсюда 
.
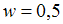Вычисляем значение выборочной средней: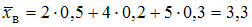
.
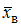называют среднее арифметическое значение признака выборочной совокупности, которое вычисляют по формул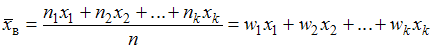е , где 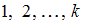– номера вариант, 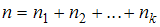– объем выборки. Наблюдаемые значения рассматриваемого признака 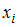называются вариантами. Количество наблюдений данной варианты – частота 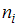. Отношения числа наблюдений к объему выборки 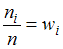называют относительными частотами.Полигоном относительных частот называют ломаную, отрезки которой соединяют точки
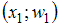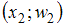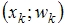, , …, . По полигону относительных частот находим координаты точек: 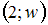; 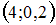, 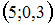. Значение неизвестной относительной частоты найдем, используя соотношение: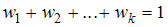, то есть 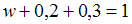, отсюда 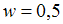.Вычисляем значение выборочной средней:
.
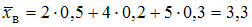