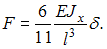Консольная балка длиной
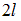нагружена силами F. Модуль упругости материала Е, осевой момент инерции сечения 
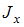заданы. Прогиб концевого сечения примет значение 
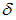, когда значение силы F равно …
- ✓
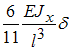
Воспользуемся универсальным уравнением упругой линии балки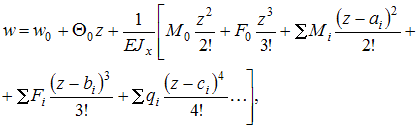 
где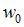
и 
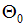– начальные параметры (прогиб и угол поворота в начале координат); 
, 
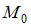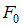– значения момента и силы в начале координат.
Составим расчетную схему. Начало координат расположим в крайнем левом сечении балки.
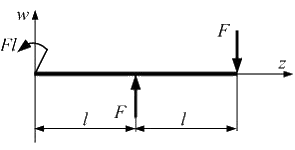
Из условий равновесия балки найдем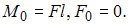
Начало координат совпадает с заделкой. В начале координат прогиб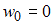
и угол поворота 
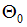=0.
Уравнение упругой линии имеет вид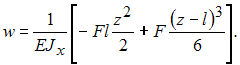
Полагая, что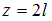
, определим прогиб свободного конца балки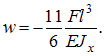 
Знак «минус» показывает, что перемещение направлено вниз.
Из условия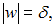
получим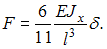 
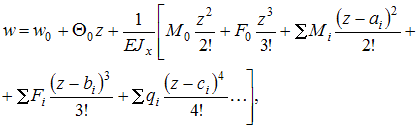
где
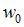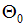и – начальные параметры (прогиб и угол поворота в начале координат); 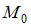, 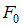– значения момента и силы в начале координат.Составим расчетную схему. Начало координат расположим в крайнем левом сечении балки.
Из условий равновесия балки найдем
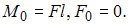
Начало координат совпадает с заделкой. В начале координат прогиб
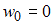и угол поворота 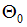=0.Уравнение упругой линии имеет вид
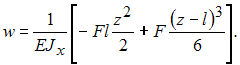
Полагая, что
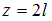, определим прогиб свободного конца балки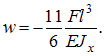 Знак «минус» показывает, что перемещение направлено вниз.
Из условия
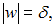получим 